ばねの伸び縮み
ロバート=フック(1635~1703年)というイギリスの物理学者はつるまきばねに重りをつるす実験をして有名なフックの法則を発見しました。
これは、つるまきばねにつるした重りの重さとつるまきばねの伸びの長さが、比例するという法則です。
つるまきばねの、下のはしに重りをさげるとばねが伸びて、下のはしがさがります。
そこで、このばねの下のはしの位置の読みを縦軸にとり重りの重さを横軸にとって、その関係をグラフにあらわすと下の図のABの直線が書けます。
この図で、伸びはA点での位置との差です。
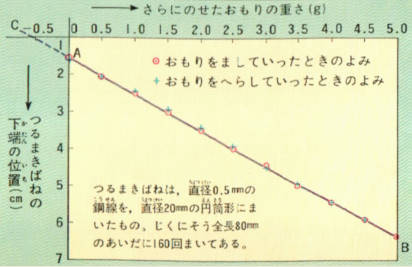
もし、つるまきばねの下のはしに上向きの力(圧縮の力)を加えてばねが縮むなら、この力に対して、ばねの縮みが比例します。
この場合の関係も、図のACの直線であらわされます。
しかし、つるまきばねでも無制限に力を増すと変形と力が比例しなくなります。材料と寸法によって、それぞれ決まった限界があります。
つぎに、つるまきばねに重りをつるしたときの力のつり合いを考えてみましょう。
上の図で、重りPの重さは、重りにはたらく重力の大きさWです。
重りは静止しているので、この重力を打ち消す力fが反対方向にはたらいていなければなりません。
この力fは、ばねが伸びたためにその内部に生じた弾性の応力によるものです。
したがって、ばねがfという力で、重りを上に引いていることになります。
もし、fより重りの重さWが大きいとするとばねはさらに下に伸びて、だんだん弾性の応力fが大きくなります。
そして、fと重力Wが等しくなったとき、ちょうどつり合います。
実験では重りの重さWと、ばねの伸びとの関係を調べましたがこれは、ばねの弾性の応力fと、ばねの伸びとの関係を調べたことと同じです。
このような実験で書いたグラフと、そのばねを使うと、重力にかぎらずほかの種類の力でも、ばねばかりの伸びによって測ることができます。
変形の種類とフックの法則
フックの法則は、つるまきばねの伸び縮みにだけあてはまるのではありません。
棒や板の伸び縮み・ねじれ・曲がりうずまきばねの軸のまわりの回転などの変形にもその材料の弾性限度内であれば、成り立ちます。
また、ずれの変形についても外から加えた力と変形の角度とのあいだに弾性限度内で、フックの法則が成り立ちます。
比例限度
弾性限度の近くでは、応力とひずみが、やや比例関係から外れてきます。
そこで、フックの法則が成り立つ限界の応力を、比例限度と言っています。
しかし、弾性限度と比例限度は、ほとんど一致すると見て差支えありません。