ねじと斜面
ねじも、斜面のはたらきを利用したものです。
ねじを見ただけでは、斜面とどんな関係にあるかよくわかりにくいので、つぎのような実験をしてみましょう。
紙を、細長い直角三角形に切って写真のように鉛筆にくるくるとまきつけます。
すると、直角三角形の長い辺(斜辺)は、ねじの形になります。
右側のものは針金を直角三角形をまくのと同じようにまきつけたものです。
こうすると、いっそうねじらしい感じがします。
このことから、ねじは、円柱のまわりに斜面をまきつけてつくったもので、ねじの山のところが、斜面にあたることがわかります。
この斜面は、ねじの一方のはしから、他のはしまで続いているのでひとまきだけ取り出して考えることにします。
ひとまきだけを取り出しても、やはり直角三角形でその高さは、下の図のBCにあたります。
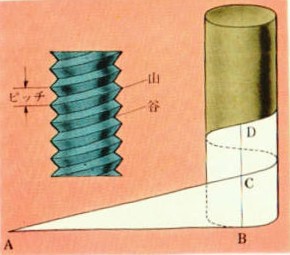
このBCの長さは斜面をもういちどまきつけて進む高さ、CDと同じです。
ですから、このねじは、1回まわるたびに小さい三角形の高さ、BCぶんだけ上へ進みます。
この長さをピッチ、または、ねじの歩みと言います。
ねじの高いところを山、低いところを谷と言います。
山と山、谷と谷のあいだの長さが、ピッチになります。
ねじのはたらき
ねじは、円柱のまわりにつくった斜面ですからそのはたらきは、斜面のはたらきと同じに考えられます。
下の図で、Aにある物は、ねじをひとまわりさせるとACの斜面にそって、Cまで上がります。
これは、ねじの1ピッチぶんだけ引き上げられたことになります。
さらにひとまわりさせると、Cにある物は、Eまで引き上げられます。
DEの高さは、BCの2倍で、ねじの2ピッチぶんにあたります。
ねじのはたらきは、このように斜面を使って物を持ち上げるのと同じです。
したがって、ピッチが小さいほど、ねじの斜面はゆるやかになりいっそう小さな力で大きな力を出すことができます。
ねじの出す力
直径が10ミリで、ピッチが2ミリのねじの出す力を考えてみましょう。
このとき、ひとまきの長さは、31.4ミリ(直径の3.14倍)になり斜面の長さは、約31.5ミリになります。
まえの図で、BCの長さが2ミリ、ACの長さが31.5ミリの直角三角形について斜面の力を考えればよいのです。
このねじに加える力は、斜面の上の物をAからCまで斜面にそって引き上げる力にあたりねじの出す力は、物をBからCまで上げる力です。
ですから、ねじに加える力と、ねじの出す力との割合は斜面の高さ(ピッチ)と、斜面の長さ(ねじのひとまわりぶんの長さ)との比であらわされます。
たとえば、このねじに1キログラムの力を加えたとすると、
1kg :(ねじの出す力)= 2 : 31.5
(ねじの出す力)= 1kg × 31.5/2 ≒ 約15.8kg
ねじの出す力は、約15.8キログラムになります。
しかし、ねじをまわすには、万力のように、多くはとってがつけてあります。
ねじの半径の10倍の長さのとってがつけてあると、直接ねじをまわすより、10分の1の力で同じ力を出させることができます。
ねじのいろいろ
ねじには、ねじの切り方や、ねじ山の形によってつぎのような種類があります。
おねじ・めねじ
円柱の外側に、直角三角形の紙をまきつけた形のものがおねじ、円筒の内側に、直角三角形の紙をまきつけた形のものが、めねじです。
言い換えると、棒になっていて、ねじこむほうがおねじ、ねじ穴が開いているほうが、めねじです。
右ねじ・左ねじ
ねじのまわる方向と進む方向から、右ねじと左ねじにおけることができます。
時計の針のまわる方向(右まわり)にまわすとまえに進むねじは、右ねじです。
これと反対に、左にまわすとまえに進むねじは、左ねじです。
ふつうのねじはたいてい右ねじで左ねじは特別の場合にしか使われていません。
三角ねじ
ボルト・もくねじなどのねじ山は、三角形をしています。
このようなねじを、三角ねじと言います。
三角ねじは小さな力でも物をしっかりと締め付けられるので、広く使われています。
もくねじのねじ山は、刃物の役目をして、仮などにくいこんでいきます。
マイクロメーターやコンパス・からすぐちなどの調節ねじも三角ねじです。
この場合は、物を少しずつ正確に動かす役目をします。
角ねじ
万力・ジャッキなどのねじは、ねじ山が四角になっています。
このようなねじを、四角ねじ、または角ねじと呼んでいます。
角ねじは、ねじに大きな力を出させるところに使います。
三角ねじを使ったのでは、ねじ山が潰れて、役に立たなくなるからです。