カテゴリー: 簡単な機械

摩擦の減らし方

摩擦は、いろいろと役に立ちますが、重い物を動かすときなどは摩擦があるために、たいへん骨が折れます。

このようなときは、できるだけ摩擦を小さくする工夫をしなければなりません。

ころと車

摩擦のうち、物が動きだすときにはたらく最大摩擦力がいちばん大きく、つぎに滑り摩擦、いちばん小さいのが転がり摩擦です。

マッチ箱を動かす実験で、マッチ箱の下に、まるい鉛筆を入れると小さな力でも、マッチ箱が動きだしました。

このように触れ合う面のあいだに、まるい棒を入れて引っ張ると転がり摩擦になるので何10分の1という小さな力で物体を動かすことができます。

このまるい棒のことをころと言います。

城の石垣を見ると、すばらしく大きな石があります。
これは、ころを使って運んだものですが、いまでも、家か動かしたり重い機械などを近くに運ぶのに、ころが使われています。

ころか使って物を運ぶには、つぎつぎところをまえにならべていかなければなりません。
この不便をなくすために、1本の軸の両はしに、輸をはめたものが車です。

また、ころの軸をかわくにとりつけて帯のようにならべたものがあります。
これは、ローラコンベアと呼ばれるもので流れ作業の進んでいる工場などで、よく使われています。

ころも車も、転がり摩擦力のほうが滑り摩擦力よりはるかに小さいことを利用したものです。

そこで、転がり摩擦について、つぎのような実験でもう少しくわしく調べてみましょう。

実験

ちょうど同じ形につくった、2本の四角い木の棒をレールのように平行にならべて、その上に、直角にころをおきます。
そして、この四角い棒と、ころのあいだの転がり摩擦を調べてみましょう。

木の棒のかわりに、2つの机を、少しはなして平行にならべその上にころを載せると回じ仕掛けがかんたんにつくれます。

まず、同じ重さの2つの重りにひもをつけてころに2,3回まきつけてつるします。

このとき、ころは、重り2つだけの重さところの重さを加えた力で木の棒を押していることになります。

つぎに、一方の重りにさげた皿に、少しずつ砂を載せていきます。
すると、ころと木の棒とのあいだに、転がり摩擦があるためしばらくは転がりませんが、砂がある重さになると、転がりはじめます。

この実験で、ころが転がりはじめたときの、砂の重さを測ります。
そして、2つの重りと、ころの重行を加えたもので、砂の重さを割るとこのときの摩擦係数がわかります。

ころと同じ材料で、同じ重さの四角い切れ端をつくり滑り摩擦係数を測ってみると転がり摩擦係数の100倍も大きいことがわかります。

軸受と油

車には転がり摩擦のほかに車軸と軸受のあいだにはたらく摩擦もあります。
車軸は軸受の中で滑りながら回転しますから、この摩擦は、滑り摩擦です。

雨戸や障子が開けにくいときろうや油をぬると、軽く開けられるようになります。
また、机や、たんすの引出が開けにくいときにも、ろうをぬります。

これは、面のでこぼこのうちへこんだところを、ろうや油がうずめて、面を滑らかにするからです。

軸と軸受のあいだには、油をさして、摩擦を小さくします。

軸を軸受に入れると、軸の両側に、角笛の形をした、隙間ができます。
ここに油を入れて、軸を回転させると油は、軸の表面にひきずられて隙間の広いところから、せまいところに向かって、流れこみます。

これは、油にねばりけ（ない）があるからです。

このとき、油に軸と軸受の触れ合う面を引き離そうとする力がはたらきます。
そのため、軸は油の上に浮いているようになり、軸と軸受の摩擦がふせげます。

油と金属とのあいだにも、摩擦はあります。
しかし、金属どうしの摩擦にくらべれば、ごく小さいものです。

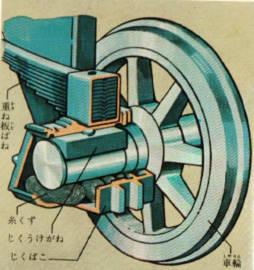
図は、貨車に使われている、軸受です。
この場合は、貨車の重みに、車軸の上からかかっています。

そこで、車軸の上側に、やわらかい貴族（ホワイトメタル）をもった軸受がねをつけています。

車軸の下には、油をしみこませた、糸くずがつめてあります。
油は、車軸が回転するにつれて、自然に車軸と軸受のあいだに入っていきます。

ボールベアリングや、ローラベアリングのように、強い圧力がかかって速く回転するものには、ねばりけの大きい、のりのようなグリースをつめ、摩擦熱によって、焼きつかないようにしています。

ボールベアリング

軸受の摩擦は、油々さすことによって、小さくすることもできますが滑り摩擦を、転がり摩擦にかえて、摩擦を小さくすることもできます。

外から見たのではわかりませんが、自転車や自動車の軸受には小さい鋼鉄の球をたくさん入れたものを使っています。

これは、ボールベアリングといって、車軸と軸受が、直接触れ合って滑り摩擦を起こすかわりに、ボールが転がって転がり摩擦になるようにしたものです。

滑り摩擦でも、転がり摩擦でも触れ合う面が滑らかでないと摩擦が大きくはたらきます。
この摩擦を小さくするには、面をできるだけ滑らかにすることが大切です。

砂利をしいた道路よりも、アスファルトやコンクリートで舗装した道路のほうが自転車や自動車が走りやすいのは、このためです。

また、汽車や電車が走るレールも、転がり摩擦を小さくするために工夫されたものです。

軸や軸受も、できるだけ滑らかに磨かなければなりません。
ボールベアリングの表面も、非常に滑らかにしてあります。

自転車や自動車では、車のまわる速さはそれほど大きくありません。
しかし、飛行機のプロペラのように、すごい速さで回転するものはボールの表面が、摩擦熱で溶けることがあります。

このようなときは、摩擦がぐっと大きくなります。
それで、高速回転をするボールベアリングについてはその材質をとくに工夫してあります。

ローラベアリング

大きな力のかかる軸受では、球のかわりに小さいころをならべた、ローラベアリングを使います。

ころは、円錐形・球面・円筒形などのものが使われています。
左の図は鉄道車両に使われている、ローラベアリングの一種です。

摩擦の利用

摩擦は、邪魔になることもあれば、役に立つこともあります。
私たちが地面を歩けるのは、地面と足とのあいだに、摩擦があるからです。

本やえんぴつを、手で握っていられるのも、摩擦があるからです。

また、ひもを結んだとき、ひとりでにとけないのも釘で板を止めることができるのも、摩擦がはたらいているからです。

このほか、摩擦を上手に利用して私たちの生活に役立てているものが、たくさんあります。

ブレーキ

自転車のブレーキは車輪のリムを硬いゴムで押しつけるようになっています。
これは、ゴムの摩擦が大きいことを利用しています。

また、もっと大きな力で車輪の回転を止めるためにハンドブレーキが使われています。

これは、摩擦の大きい石綿を材料にしてつくった帯（ブレーキバンド）で、鋼鉄の輪をしめつけるものです。

スクーター・オートバイ・自動車などのように速く走る乗り物を止めるためにはさらに大きな摩擦力を出さなければなりません。

そこで、鋼鉄製のブレーキドラムの内側に固い石綿織物をはったブレーキシューを大きな力で押しつけるしくみを使っています。

また、汽車や電車などでは、制輪子という鉄を車輪に押しつけて止めます。

スノーチェーン

雪が降ると、バスなどの自動車は、タイヤにチェーンをまきつけます。

これは、雪によって、タイヤがスリップしやすくなるためにタイヤにチェーンをまきつけ、道路とのあいだの摩擦を大きくして滑らないようにするためです。

チェーンのついていない自動車は、スリップしてたいへん危険です。

このように、摩擦は、私たちの生活に上手に利用されています。

滑り摩擦

スキーでもスケートでも、滑りはじめには最大摩擦力に打ち勝たなければならないので、大きな力を必要とします。

しかし、滑っているあいだは、運動摩擦力がはたらいているのであまり力を加えなくても滑り続けます。

このように、ある面を滑るときの摩擦を運動摩擦のうちでも、とくに滑り摩擦と言います。

転がり摩擦

まえの摩擦用の箱の実験で摩擦用の箱のかわりに斜面用のトロッコをつないでみます。
すると、さらの重さだけでトロッコは動きはじめます。

この場合、トロッコが板の面を転がって動きます。
このときの摩擦を、転がり摩擦と言います。

転がり摩擦力は滑り摩擦力より、さらに小さいので摩擦を減らす方法として機械の部分などに広く利用されています。

摩擦係数

摩擦用の箱で、板と接する面をいろいろかえてみると最大摩擦力は、まえと違った大きさになります。
つまり、箱の4つの面のうち2面は同じ性質で、接している面積が違います。

箱の広い面を接するときと、せまい面を接するときの実験をしてみるとせまい面のときの最大摩擦力と広い面のときの最大摩擦力は同じ大きさになります。

これらの実験から、最大摩擦力は、触れ合う表面の性質によって大きさが違いますが、面の広さには関係がないことがわかります。

つぎに、箱の上に分銅をのせて、重さをまえの2倍にし同じように最大摩擦力を測ってみると、2倍になっているのがわかります。

皿に分銅を増やして、摩擦用の箱を重くすると最大摩擦力も、それに比例して増えていきます。

このことから、最大摩擦力は、2つの面の押し合う力に比例していることがわかります。

紙の面と、紙やすりの面とでは、最大摩擦力が違います。
それは、表面の性質が違うからです。
この表面の性質は、摩擦係数という数であらわします。

図のような実験をしてみましょう。

箱が動きだす瞬間は、箱を引く力Ｐと最大摩擦力Ｑとは等しくなります。
触れ合っている2つの面の押し合う力を、ＲとＳとしますとＱの力とＳの力の比を、摩擦係数と言います。

同じ重さの物なら、摩擦係数の大きい物ほど動かすのに余計に力がいります。
また、動いているときでも、重い物ほど、大きな摩擦力がはたらきます。

上の表は、いろいろな物の、摩擦係数をあらわしたものです。
触れ合う面の違いによって、摩擦係数の大きさもだいぶ違うことがわかります。

摩擦の起こるわけ

2つの面のあいだに、どうして摩擦が起こるのでしょうか。
これについては、つぎのような原因が考えられています。

①　2つの面の直接ふれあう部分がくっついてしまい、それを引き離すのに、力がいる。

②　物の表面は、どんなに滑らかに見えても非常に細かいでこぼこがあり、これが互いに噛みあうので、それを乗り越えたり引きちぎったりするために、力がいる。

③　硬い面が、柔らかい面の上にあるときは硬い面が、柔らかい面を掘り起こしたり、壊したりするために力がいる。

この様子は、触れ合う物によって、それぞれ違うので摩擦力の大きさも、いろいろかわるのです。

摩擦力

机の上にある本やスタンドを、軽く押してごらんなさい。
わずかの力で押したのでは動きませんが、強く押すと動き出します。

物を動かすには、力を加えなければなりません。
しかし、加える力が、ある大きさより小さいとこのように物が動かないことがあります。

力を加えているのに物が動かないほかの例を考えてみましょう。

ふたりが向き合って、1本の棒を両はしから互いに押したとします。
ふたりの押す力の大きさが等しくて向きが反対なので棒はどちらへも動きません。

机の上の物も、これと同じです。
物を押しても動かないのは、動かす方向と反対に別の力がはたらいていて、動くのを止めているからです。

このときの力は、目には見えませんが触れ合っている2つの物の面のあいだにはたらいている力で摩擦、または、摩擦力と言います。

このように、摩擦力は、物の運動をさまたげる方向にはたらくので摩擦力より大きな力で押したり引いたりしなければ物を動かすことはできません。

雪や氷の上では、よく滑ります。これからです。

しかし、スキーで滑る場合でも、板の上ならともかく平地で滑るときには、ときどき手や足に力を加えて加減しないと続けて滑ることができません。

力を加えないでいると、まもなく止まってしまいます。

このことから、滑っているときでも運動をさまたげろ力は小さいけれども、
はたらいてしることがわかります。

走っている自動車や電車は、動きだしてからもたえずエンジンやモーターをはたらかせています。
これは摩擦力によって、自動車や電車の運動が絶えずさまたげられているためです。

このように、摩擦力は物が止まっているときばかりでなく滑っている物や転がっている物にもはたらいてその動きを止めようとしています。

実験

摩擦力の大きさを調べるには、図のような摩擦実験装置を使います。

摩擦用の箱は、4つの面がそれぞれすべすべする金属の面と金属に紙をはった面、紙やすりをはった面、もう1つの面は板に接している面積が少なくなっています。

摩擦用の箱と皿を、滑車を通して写真のようにつなげます。
つぎに、箱が滑り出すまで、さらに分銅を載せていきます。

このとき、摩擦用の箱には、分銅と皿の重さのために上の図のようにＰという水平な力がはたらきますが、まだ動きません。

これは、Ｑのような水平で、Ｐと反対向きの摩擦力がはたらきＰとつりあっているからです。

さらの分銅を増やせば増やすほど、箱を引く力Ｐは大きくなります。
しかし、摩擦力もだんだん大きくなります。
この2つの力の大きさが同じで、いつもつりあっているときは箱は動きません。

摩擦力の大きさは、面の材質によってもまた、斜面の角度によっても、かわってきます。

静止摩擦力

物体が止まっているときの摩擦はその物体を引く力と大きさが等しく向きが反対です。

たとえば、1キログラムの力で引いても動かないときは1キログラムの摩擦力がはたらいているわけです。

まえと同じ実験で、ある重さまで分銅を載せると、ついに箱が動きはじめます。

摩擦力は、これ以上大きくなりません。
つまり、摩擦力は、箱が動きはじめようとするときが、いちばん大きいのです。

物体が止まっているときに、はたらく摩擦力を静止摩擦力と言い物体が動きだす瞬間のいちばん大きな摩擦力を最大（静止）摩擦力と言います。

最大摩擦力の大きさは、このときの皿と分銅の重さと等しくなります。
したがって、それを測りで測れば、最大摩擦力がわかります。

運動摩擦力

静止摩擦力に対し、物体が動いているときにその動いている物体を止めようとする摩擦力を運動摩擦力と言います。

運動摩擦力は、最大摩擦力より小さくなっています。

この運動摩擦力の大きさは物体の速度の大きさにはほとんど関係かわりません。

ねじと斜面

ねじも、斜面のはたらきを利用したものです。
ねじを見ただけでは、斜面とどんな関係にあるかよくわかりにくいので、つぎのような実験をしてみましょう。

紙を、細長い直角三角形に切って写真のように鉛筆にくるくるとまきつけます。

すると、直角三角形の長い辺（斜辺）は、ねじの形になります。
右側のものは針金を直角三角形をまくのと同じようにまきつけたものです。
こうすると、いっそうねじらしい感じがします。

このことから、ねじは、円柱のまわりに斜面をまきつけてつくったもので、ねじの山のところが、斜面にあたることがわかります。

この斜面は、ねじの一方のはしから、他のはしまで続いているのでひとまきだけ取り出して考えることにします。

ひとまきだけを取り出しても、やはり直角三角形でその高さは、下の図のＢＣにあたります。

このＢＣの長さは斜面をもういちどまきつけて進む高さ、ＣＤと同じです。

ですから、このねじは、1回まわるたびに小さい三角形の高さ、ＢＣぶんだけ上へ進みます。
この長さをピッチ、または、ねじの歩みと言います。

ねじの高いところを山、低いところを谷と言います。
山と山、谷と谷のあいだの長さが、ピッチになります。

ねじのはたらき

ねじは、円柱のまわりにつくった斜面ですからそのはたらきは、斜面のはたらきと同じに考えられます。

下の図で、Ａにある物は、ねじをひとまわりさせるとＡＣの斜面にそって、Ｃまで上がります。
これは、ねじの1ピッチぶんだけ引き上げられたことになります。

さらにひとまわりさせると、Ｃにある物は、Ｅまで引き上げられます。
ＤＥの高さは、ＢＣの2倍で、ねじの2ピッチぶんにあたります。

ねじのはたらきは、このように斜面を使って物を持ち上げるのと同じです。
したがって、ピッチが小さいほど、ねじの斜面はゆるやかになりいっそう小さな力で大きな力を出すことができます。

ねじの出す力

直径が10ミリで、ピッチが2ミリのねじの出す力を考えてみましょう。

このとき、ひとまきの長さは、31.4ミリ（直径の3.14倍）になり斜面の長さは、約31.5ミリになります。

まえの図で、ＢＣの長さが2ミリ、ＡＣの長さが31.5ミリの直角三角形について斜面の力を考えればよいのです。

このねじに加える力は、斜面の上の物をＡからＣまで斜面にそって引き上げる力にあたりねじの出す力は、物をＢからＣまで上げる力です。

ですから、ねじに加える力と、ねじの出す力との割合は斜面の高さ（ピッチ）と、斜面の長さ（ねじのひとまわりぶんの長さ）との比であらわされます。

たとえば、このねじに1キログラムの力を加えたとすると、

1kg :（ねじの出す力）＝ 2 : 31.5

（ねじの出す力）＝ 1kg × 31.5/2 ≒ 約15.8kg

ねじの出す力は、約15.8キログラムになります。
しかし、ねじをまわすには、万力のように、多くはとってがつけてあります。
ねじの半径の10倍の長さのとってがつけてあると、直接ねじをまわすより、10分の1の力で同じ力を出させることができます。

ねじのいろいろ

ねじには、ねじの切り方や、ねじ山の形によってつぎのような種類があります。

おねじ・めねじ

円柱の外側に、直角三角形の紙をまきつけた形のものがおねじ、円筒の内側に、直角三角形の紙をまきつけた形のものが、めねじです。
言い換えると、棒になっていて、ねじこむほうがおねじ、ねじ穴が開いているほうが、めねじです。

右ねじ・左ねじ

ねじのまわる方向と進む方向から、右ねじと左ねじにおけることができます。

時計の針のまわる方向（右まわり）にまわすとまえに進むねじは、右ねじです。

これと反対に、左にまわすとまえに進むねじは、左ねじです。
ふつうのねじはたいてい右ねじで左ねじは特別の場合にしか使われていません。

三角ねじ

ボルト・もくねじなどのねじ山は、三角形をしています。
このようなねじを、三角ねじと言います。

三角ねじは小さな力でも物をしっかりと締め付けられるので、広く使われています。
もくねじのねじ山は、刃物の役目をして、仮などにくいこんでいきます。

マイクロメーターやコンパス・からすぐちなどの調節ねじも三角ねじです。
この場合は、物を少しずつ正確に動かす役目をします。

角ねじ

万力・ジャッキなどのねじは、ねじ山が四角になっています。
このようなねじを、四角ねじ、または角ねじと呼んでいます。

角ねじは、ねじに大きな力を出させるところに使います。
三角ねじを使ったのでは、ねじ山が潰れて、役に立たなくなるからです。

くさびのはたらき

斜面を使うと、小さい力でも、重い物を引き上げることができます。
つまり、小さい力で大きな力を出したことになります。

くさびは、この斜面の性質を利用したものです。

くさびのきり口は、たいてい2つの辺の等しい、細い三角形をしています。
この二辺にはさまれた角をくさびの角、短い一辺をくさびの頭と言います。

下の図をごらんなさい。

ハンマーなどで、くさびの頭にＰの力を加えるとこの力は、くさびの斜辺に直角な2つの力、ＱとＲとにわかれます。

この力が、木を折るときの力になります。

この3つの力のあいだにも、斜面のときと同じように力の平行四辺形があてはまります。
平行四辺形の対角線Ｓは、Ｐと同じです。

この平行四辺形の半分の三角形は、くさびと同じ角度をもっているのでＲとＳの大きさの割合は、くさびの斜面と頭の長さの割合に等しくなります。

（Ｒの力）：（Ｓの力）＝（斜面の長さ）：（頭の長さ）

Ｒの力は、くさびの出す力ですから、これを式であらわすと、

Ｒ……くさびの出す力
Ｓ……加えた力

この式からわかるように、くさびの頭の長さが、斜面にくらべて短いほど、くさびは大きな力を出すことができます。

たとえば、くさびの斜面の長さが、頭の長さの5倍あったとします。
このくさびに1キログラムの力をはたらかせると5キログラムずつの力となって、2つの斜面からはたらきます。

くさびと刃物

斧や、包丁などは、その切り口を見るとちょうどくさびと同じ形をしています。

物を割ったり、切ったりするときの力のはたらき方も、くさびと同じです。

刃物は刃がうすいほど、切れ味がよくなります。
それは、くさびの角度が小さいほど、くさびの出す力は大きくなるからです。

しかし、刃がうすいと折れやすくなるので使い道によって、いろいろとかわった形にしています。

くわ・すき・つるはし・スコップなど地面を掘り起こす道具もくさびと同じに考えられます。

これらの道具の形と厚さ、えと刃の角度、地面の硬さなどとの関係を調べてみるのも、おもしろいでしょう。

かんな・のみなど、材料に食い込んで削っていくときの力のはたらき方も、くさびと同じです。

包丁やナイフは、ただ上から押しつけて切るよりも押したり、引いたりするほうが、よく切れます。

下の図をごらんなさい。

包丁を手もとに引きながら切ると、包丁の動きは、Ｒの方向になります。
このときのくさびの形は、（Ａ）のようになります。
包丁を、ただ上から押したときのくさびの形は（Ｅ）です。

この2つのくさびを調べると、くさびの頭の長さは同じでも手もとに引いたときのほうが、斜面の長さはずっと長いことがわかります。

斜面が長くなると、くさびの角度は小さくなりますからよく切れることになるのです。

斜面の力をもとめる方法

まえの実験からでは、摩擦があるので正しい力の大きさをもとめることはできません。
そこで、斜面にそって落ちる力を正しくもとめる方法を考えてみましょう。

斜面の力をもとめる方法には、図を書いてもとめる方法と計算でもとめる方法の2通りがあります。

図を書いてもとめる方法

この方法は、力の大きさをあらわすのに矢印を使い、矢印の方向は力がはたらいている方向とします。

矢印の長さは、力の大きさの割合をあらわすように書きますたとえば、1キログラムを1センチの長さであらわしたとすると5センチの矢印は、5キログラムをあらわすものとします。

下の図のように、斜面の傾きを30度として斜面の上に3キログラムの物体を載せます。

この場合、物体にはたらく重力のＷは、真下に向かってはたらきます。
このとき、０Ｗの力は、斜面にそって落ちようとする力ＯＰと物体が斜面に垂直におさえつける力ＯＱの2つの力に分解されます。

このＯＱという力の反作用として、抗力ＯＱ’がはたらいています。

重力ＯＷを対角線としＯＰとＯＱの力を二辺とする平行四辺形をつくってみます。
ＯＷの長さとＯＰとＯＱの長さを測ると力の大きさの割合がもとめられます。

たとえば、上の図で斜面の上に3キログラムの物体の重力ＯＷを3センチであらわしたとするとＯＰの力の大きさは、15センチであらわされます。

また、45度の斜面の上の物体は下の図のように30度の斜面の上の物体よりも滑りやすくなります。

これは、30度の斜面の上においた物体と同じ重さの物体を45度の斜面の上に置いてみるとわかります。

つまり、30度のときのＯＰと45度のときのＯＰとでは45度のときのＯＰのほうが大きいのです。

計算でもとめる方法

ＯＰの力は、計算によっても、もとめることができます。

物体の重さの中心をＯとして、まえと同じような図を書いてみましょう。
重力ＯＷの矢印と、斜面にそって落ちようとする力ＯＰの矢印と出てきた三角形ＯＷＰをもとの三角形ＡＢＣとくらべてみましょう。

この2つの三角形では、角Ｂと角Ｗが30度、角Ａと角Ｏが60度、角Ｃと角Ｐが直角でそれぞれ等しくなっています。
この2つの三角形は、3つの辺の長さの割合が同じになります。

つまり、ＯＷの力とＯＰの力の大きさの割合は斜面をつくっている三角形ＡＢＣの、傾いた辺の長さ（ＡＢ）と垂直の辺の長さ（ＡＣ）との割合に等しくなります。

これを比例式であらわすと　〇Ｗ　:　ＯＰ = ＡＢ　:　ＡＣ　となります。

これを変形すると　ＯＰ＝ＯＷ × ＡＣ/ＡＢ　となります。

たとえば、30度の傾きをもった斜面ではＡＢの長さと、ＡＣの長さの割合は、2対1です。
いま、この斜面に3キログラムの物体をのせると　ＯＰ＝ 3(kg) × 1/2 ＝ 1.5(kg) となりまえと同じく、1.5キログラムになります。

傾いた辺の長さと、垂直の辺の長さを測って、その割合をもとめておくと、ＯＷがどのような値でも、ＯＰがもとめられます。

斜面と仕事

斜面を使って、物体を引き上げたときにする仕事もてこや滑車・輪軸を使ったときにする仕事と、原理は同じです。

つまり、力では得をしていますが、距離で損をしています。

たとえば、4キログラムの物体を人の手で1メートル持ち上げたときにした仕事の量は　4(kg）× 1(m）= 4(kgm) となります。

これを30度の斜面で引き上げたときの仕事を考えてみましょう。
斜面の上に4キログラムの物体を落ちないように支えるには、上の公式から　Pの力 ＝ 4(kg) × 1/2 ＝ 2(kg)　で、つまり、2キログラムの力で反対の向きにくわえればちょうどつり合うことになります。

30度の斜面の距離は、高さの2倍の距離がありますから1メートル上げるには、斜面の上を、2メートル動かさなければなりません。

ですから、30度の斜面で、物体を1メートル引き上げたときの仕事の量は、　2（kg)× 2(m）= 4(kgm）となります。

したがって斜面を使わないで、物体を持ち上げるときにする仕事も斜面を使って、それと同じ高さまで物体を引き上げるときにする仕事も仕事の量としては、かわりがありません。

しかし、実際には、斜面を使った場合には斜面と物体とのあいだで、摩擦がはたらいているのでその分だけ余計に力が必要です。

図は、物体の重さが一定なときに、斜面の角度をかえることによって引き上げるときの力の大きさの違いを、矢印であらしわしたものです。

斜面

平らな道を歩くときよりも坂道をのぼるときのほうが余計に疲れます。
急な坂道をのぼるよりも傾斜のゆるやかな坂道のほうが疲れは少なくてすみます。

たとえば、山にのぼるとき、頂上がすぐ目の前に見えてしてもまっすぐに頂上までのぼろうとするには、たいへんな労力が必要です。

そこで、多くの人が遠まわりをしてでも傾斜のゆるやかな道を選んで、のぼるわけです。

そのほうが、歩く道のりは長いけれども疲れは、ずっと少なくてすむからです。

スキーで、雪の上を滑るときは、どうでしょうか。
平らなとこらでは、自然に滑るわけにはいきません。
ところが、斜面にそって滑ると、勢いよく雪を蹴って進みます。

このように坂道は平地と違っていろいろなはたらきをすることがわかります。

坂道は、必ず、ある角度の傾きを持っています。
このように、傾いている面を斜面と言います。

斜面にはたらく力

私たちは大きいカを出すと疲れますが小さい力では、それほど疲れません。
坂逆を歩くときに平地を歩くときよりも、余計に疲れるのはそれだけ大きい力を出しているからです。

平らな机の上に、滑りやすい物または、転がりやすい物をおいても、そのままの位置で止まっています。

ところが斜面の上におくと自然に斜面にそって滑り落ちたり、転がり落ちたりします。

斜面の上では、このように力を加えなくても自然に物を動かす力がはたらいています。

これは、物が真下に落ちようとすると斜面が邪魔をするため、真下に落ちず、斜面に沿って下に落ちるからです。

物体が真下に落ちる速さと、斜面に沿って落ちる速さとをくらべてみると、斜面に沿って落ちるほうが、ずっと遅いことに気がつきます。

斜面の角度をいろいろかえると斜面に沿って落ちる速さがまわります。
それは、斜面の角度によって斜面にそって物体にはたらく力がかわるからです。

実験

写真のような斜面の実験装置を用意します。

①　まず、45度の斜面で実験してみましょう。
重りのいろいろかえて、斜面の上の物とつり合わせると
物体は上にも下にも動かないで止まります。

②　つぎに、斜面の角度をだんだん小さくして
30度にした場合を考えてみましょう。

重りの重さはそのままで、斜面の角度を、かえただけです。
この場合、斜面の上の物体が、斜面の上部にのぼっています。

③　今度は斜面の角度を大きくして、角度を60度にしてみましょう。
斜面の上の物体は、30度の場合とは反対に、斜面の下部へ落ちています。

④　斜面の角度が直角（90度）になったときは
ちょうど物体をつりあげたときと同じになります。

したがって、斜面の上の物体が下に落ちようとする力は
このときがいちばん大きくなります。

また、重りの重さが、斜面の上の物体の重さと等しいとき、つりあいます。
右の図は、45度・30度・60度・直角の斜面の実験を1つにしたものです。

これらの実験で、斜面の角度が、大きくなるほど
斜面にそって落ちようとする力も大きくなることがわかります。

水平面にある物体は、ある方向に力を加えないと動きませんが
斜面の上では、力を加えなくても自然に動きます。

これは地球に物体を引き寄せる力が、はたらいているからです。
そのため、地球上の物体は、必ず地表に落ちます。
物体にはたらく下向きの力で物体の重さとなる力を重力と言います。

滑車の利用

私たちの生活には、いろいろのところに、滑車が利用されています。
校庭の旗竿の先や、鯉のぼりを上げる竿の先には定滑車が使ってあります。
いまでも、農村に行くと見られる車井戸も、定滑車です。

このほか、工場・駅・建築工事場・港などで見られるクレーンや重い物を持ち上げるチェーンブロックにも組み合わせ滑車が使われています。

クレーン

重い荷物を軽々と持ち上げて、右へ左へと自由に運ぶクレーンは滑車と輪軸のはたらきを、上手に組み合わせてあります。

クレーンには、いろいろの種類がありますがはたらきの原理は、みな同じです。

自由に傾きをかえられる腕の先に定滑車と動滑車を組み合わせたものが、つるしてあります。

上の写真は、定滑車と動滑車を上手に利用したしゅんせつ船です。
これには、動滑車についているかぎ（フック）のかわりに川底の土や砂をさらう腕が取り付けてあります。

港で荷物を積み下ろしするクレーンも大きな鉄の枠に滑車と輪軸のしくみが取り付けてあって全体がレールの上を動くようになっています。

上の写真は、港の倉庫に取り付けられた壁クレーンです。
船から直接倉庫に入れられるようになっています。

チェーンブロック

これは歯形をつけた組み合わせ滑車でロープのかわりにチェーンが使ってあります。

チェーンは、1つの輪になっていて歯形をつけた滑車とかみ合っているため、チェーンから手をはなしてもつり下げてある物が、落ちるようなことはありません。

ひとりの力でも、重い荷物を持ち上げられるので便利です。

滑車と仕事

滑車を使うと、力で得をしたり力の方向をかえることができることがわかりました。

動滑車を1つ使って重りを上げる場合には、ひもを引く力が重りの重さの半分の力ですみますから、力で得をしていることになります。

しかし、重りを10センチ上げるにはひもを2倍の20センチ引き上げなければなりません。

また、定滑車を用いると力の方向がかわるだけで力の大きさの損得はありません。

したがって、10グラムの重りを10センチだけ上げるには20グラムの力で、10センチだけたぐればよいのです。

定滑車と動滑車の仕事

動滑車のひもの一方は同定されています。

他方のひもを引き上げるとき、固定されている方のひもの分までつり上げなければならないため、ひもを引く長さは重りを上げる距離の2倍かかります。

これを、動滑車の仕事の量で考えてみましょう。

仕事の量は、物体におよぼした力の大きさとその力によって物体が動いた距離との積であらわします。

ですから、動滑車を使ったときの仕事の量はつぎのような式であらわすことができます。

（重りの重さの1/2倍の力）×（重りが動いた距離の2倍）＝（重りの重さに等しい力）×（重りが動いた距離）

となります。

ですから、仕事の量には、かわりがありません。
したがって、動滑車を用いないで重りを上げる場合も動滑車を用いる場合も、仕事に損得はありません。

定滑車を用いたときの仕事は重りの重さに等しいカで重りが動いた距離だけ動かせばよいので、定滑車の仕事の量はつぎのような式であらわされます。

（重りの重さに等しい力）×（重りが動いた距離）

したがって、定滑車の場合にも、仕事に損得はありません。

たとえば、10キログラムの荷物を2メートル持ち上げたときの仕事の量は10(kg）× 2（m）＝ 20(kgm）　となります。
　
これを、定滑車を用いて、滑車に仕事をさせるときは10キログラムの荷物を滑車が上向きに2メートルほど動かすことになります。

つまり、滑車が荷物に、10(kg)× 2(m）＝ 20（kgm）の仕事をしたわけです。

滑車が、荷物に仕事をするためには人が滑車にそれだけの仕事をしなければなりません。

定滑車の場合、人が、ひもを引く力の大きさは荷物の重さに等しいカで2メートルだけ下に引っ張ればよいのですから10（kg）× 2（m）= 20（kgm）の仕事を、人が定滑車にしています。

動滑車の場合には、10キログラムの半分の力でひもを引く距離は荷物が動いた距離の2倍の距離ですから。

10(kg) × 1/2 × 2(m) × 2 ＝ 20(kgm)の仕事を、人が動滑車にしています。

組み合わせ滑車の仕事

定滑車と動滑車を組み合わせた滑車では動滑車を使うことによって、力で得をして距離で損をしています。

定滑車を使うことによって、力の方向がかわるだけで力でも距離でも損得はありません。

たとえば、下の右図のように、定滑車1つと、動滑車1つの組み合わせ滑車で、40キログラ厶の重りを、1メートル上げたとき、組み合わせ滑車がする仕事は、つぎのようになります。

40（kg）× 1(m）＝ 40（kgm）

滑車が、それだけの仕事をするには人が滑車にそれだけの仕事をしなければなりませんから仕事の量は40(kg) × 1/4 × 1(m) × 4 ＝ 40(kgm)となります。

また、定滑車と動滑車をそれぞれ3つずつ組み合わせた滑車では滑車が60キログラムの重りを1メートル引き上げたときの仕事の量は60キログラムメートルです。

滑車が、重りにそれだけの仕事をしたわけですから人が、それだけの仕事をしなければなりません。

ですから、滑車を使っても、仕事で得したということはありません。
このことは、滑車にかぎらず、てこ・斜面・輪軸などの場合にも成り立っています。

人が機械を利用するのは、仕事で得をするためではなくて力が距離で得をするためです。

実際には、摩擦がありますから機械が物体にする仕事よりも少し大きな仕事を、人が機械にあたえなければなりません。

ひもを斜めに引いたときの仕事

今までは、物体にはたらいている力の向きに、物体が動く場合でした。
ところが物体が動く方向と力の向きが、違っている場合もあります。

定滑車で、重りを引き上げるとき、ひもを引く力は、引く方向に関係なく、重りの重さと等しい力で、引っ張ればよいわけです。

ところが、動滑車で、重りを引き上げるときは、ひもを引く力の大きさが、引く方向によって違っています。

動滑車の場合、ひもを引く方向が、鉛直方向であるときは引く力の大きさが、重りの重さの半分でよいのですが図のような方向に引くときは、力の大きさが重りの重さの半分より大きくなります。

これは、固定されているひもが、支点の役目をしているからです。
したがって、動滑車の場合、ひもを引く方向が、鉛直方向であるときがひもを引く力の大きさは、いちばん小さくてすみます。

滑車の組み合わせ

動滑車を使うと、力を得することができますが、重りを上にあげるには滑車のひもを、上に引き上げなければなりません。

また、定滑車を使うと力で得することはありませんが力の向きをかえることができます。

そこで、定滑車と動滑車を、いくつか組み合わせると両方のはたらきをいっしょにすることができ、たいへん便利になります。

つぎに、いろいろの滑車の組み合わせについて、調べてみましょう。
しかし、滑車の重さや摩擦などは、考えに入れないことにします。

動滑車1つと定滑車1つ

この組み合わせでは、動滑車のはたらきで力の得をして、定滑車のはたらきで、力の方向をかえます。

組み合わせ方は、上の写真のように2通りありますが原理は、どちらも同じです。

動滑車を用いると、ひもを引く力は滑車と重りの重さの半分でよいわけですが滑車の重さを考えにいれなければ、ひもを引く力は重りの重さの半分でよいわけです。

定滑車1つだけでは、力の方向をかえるだけで力を得することはできませんから、この組み合わせ滑車を用いるとひもを引く力は、動滑車1つを使ったときと同じ力に等しいわけです。

たとえば、この組み合わせで、100グラムの重りを引き上げるには50グラムの力で引けばよいことになります。

動滑車2つと定滑車1つ

まえの動滑車1つと定滑車1つの組み合わせに下の図のように動滑車を、もう1つ加えた組み合わせ方です。

重りをつるしてある第一の動滑車のひものはしは第二の動滑車の軸につるしてあり、第二の動滑車のひものはしは定滑車にを通してあります。

第一の動滑車から第二の動滑車にかかるひもＡには重りの重さの半分の力が加わります。

また、第二の動滑車から定滑車にかかるひもＢにはＡにかかる力の、さらに、半分の力がかかることになります。

この組み合わせ滑車で第一の動滑車に100グラムの重りをつるしたとき、その重りを引き上げるには

（重りの重さ）× 1/2 × 1/2 ＝ 引く力

の大きさの力で、すむことになります。
つまり、

100 × 1/2 × 1/2 ＝ 25

で、25グラムの力で引けばよいわけです。左の写真は、さらに、動滑車1つを加えたものです。

第一の動滑車のはたらきで、重りの重さは2分の1に第二の動滑車のはたらきで、さらにその2分の1になり第三の動滑車のはたらきで、さらに2分の1になります。

ですから、ひもを引く力は、

（重りの重さ）× 1/2 × 1/2 × 1/2 ＝ 引く力

の大きさの力となります。

このような組み合わせ滑車では動滑車の数を、4つにしても、5つにしても同じような考え方でよいわけです。

定滑車3つと動滑車3つ

下の図のように、定滑車3つと動滑車3つを組み合わせた滑車では動滑車を支えている6本のひもには、それぞれみな同じ力がかかります。

というのは、動滑車にかかるそれぞれのひもがみな重りをつるしていることになるからです。

したがって、1本のひもにかかる力は、重りの重さの6分の1になります。

この組み合わせ滑車では、ひも1本にかかる力はひもの数が多くなるほど、つまり、滑車の数が多くなるほど小さくなります。

いま、図の動滑車に、60グラムの重りをつるしたとき定滑車のひもを引く力は60グラムの6分の1、10グラムの力で引けばよいのです。

定滑車2つと動滑車2つ

この組み合わせ滑車では、定滑車は定滑車で動滑車は動滑車で、1つの軸を縦にならべたものです。

下のＡ図で、定滑車の軸の下につるしたひもは小さい動滑車を通して小さい定滑車へ大きい動滑車を通して大きい定滑車へと1本のひもで定滑車と動滑車のあいだを往復させた組み合わせ滑車です。

動滑車をつるしているひもは、全部で4本ありますから1本のひもには重りの重さの4分の1の力がはたらいていることになります。

たとえば、Ａ図のように、40グラムの重りを引き上げるには動滑車をつるしている4本のひもに、それぞれ10グラムの力がはたらいているわけです。

したがって、10グラムの力でひもを下に引っ張ればよいことになります。

動滑車2つと定滑車3つ

Ｂ図のように、ひものはしを動滑車の軸の上につるすと定滑車は1つ増えることになります。

Ｂ図の組み合わせ滑車が、Ａ図のそれと違うところは定滑車が1つ増えたことですが、定滑車が1つ増えることによって動滑車をつっているひもの数が1本増えることになります。

ですから、この組み合わせ滑車にＡ図の組み合わせ滑車につるした重りと、同じ重さの重りをつるすと定滑車が1つ増えただけ、力は小さくてすみます。

40グラムの重りをつるしたときひもを引っ張る力は、5分の1の8グラムでよいわけです。

このような組み合わせ滑車では、ひもを引っ張る力の大きさは動滑車をつっているひもの本数によってかわってきます。

つまり、同じ重さの重りをつるし上げるにはひもの本数が多ければ多いほど、力は小さくてすみます。

したがって、ひもを引っ張るときの力の大きさを考えるときは動滑車をつっているひもの本数を数えそれらのひも1本1本に重りの重さがかかっていることを考えに入れなければなりません。

定滑車3つと動滑車3つ

さらに定滑車1つと動滑車1つを増やして定滑車3つと動滑車3つの組み合わせ滑車を考えてみましょう。

Ａ図の組み合わせ滑車もＢ図の組み合わせ滑車も同じ数だけの定滑車,動滑車とを用いた組み合わせ滑車ですがＡ図では滑車を縦にならべ、ひもの組み方をわかりやすくしたもので、Ｂ図では、共通の軸を持たせ、定滑車は定滑車どうし動滑車は動滑車どうしでいっしょにしたものです。

この2つの組み合わせ滑車は、いずれもひものはしが定滑車の軸の下につないであります。

動滑車をつっているひもの本数は、全部で、6本ありますから重りの重さは、それぞれひも1本1本に等分され1本のひもにかかる力の大きさは、重りの重さの6分の1になります。

たとえば、600グラムの重りをつるすには6本のひもにそれぞれ100グラムずつの力がはたらいているので100グラムの力ですむにわけです。

このように、組み合わせ滑車では力の大きさがひもの多少によって、違います。

定滑車と動滑車

溝のついた車が、軸のまわりをまわれるようにしたものを滑車と言います。
この滑車は、使い方によって、2つの種類にわけられます。

滑車の軸を、動かないように、しっかりと枠に取り付けて溝にかけたひもを引くと車だけがまわるようにしたものを定滑車と言います。

また、軸が動くようになっていて、ひもをひくと、車がまわりながら
滑車全体が動くようにしたもりを動滑車と言います。

私たもの使っている機械には滑車のはたらきを利用したものが、たくさんあります。

定滑車のはたらき

定滑車にかけたひものはしに重りを結びつけてもう一方のはしをひくと重りがあがっていきます。

ひもをひく力は、下向きにはたらいていますがこの力が、ひもを通して重りに伝えられるときには上向きの力になっています。

このように定滑車では、上から下へひっぱる力で重りを下から上へ持ち上げるわけですから力の方向をかえるはたらきをします。

下向きの力で、重りを上にひきあげることができるのは私たちにとって、たいへん便利なことです。

もし、重りにひもをつけて、直に上にひきあげなければならないとすると、自分が高いところにのぼっていなければなりません。

そのうえ、悪い足場で、不自由な姿勢で力を出さなければならないので大きな力は出せません。

ところが、定滑車を使うと、便利な足場を、自由に選ぶことができます。
また、自分の体重を利用して、ひもをひけばよいわけですから楽に大きな力が出せることになります。

それでは、ひもをひく力は、どれほどいるでしょうか。

写真のように、ひもの両はしに同じ重さの重りをつけるとつりあって動きません。
しかし一方の重りを、ほんの少しだけ増してももう一方の重りが引き上げられます。

このことから、ひもをひく力は重りの重さと同じでよいと考えられます。

定滑車は、ちょうど真ん中が支点になっているてこと考えることができます。

支点から作用点までの距離と、力点までの距離は、滑車の半径です。
このようなてこは、両側の力が等しいときに、つり合います。

動滑車のはたらき

動滑車では、力の向きはかえられませんが力の得ができます。
このわけを、下の写真のようにして、調べてみましょう。

まず、①の写真のように重りを滑車につるして全体の重さを、ばねばかりで測ります。

つぎに、②の写真のように滑車にひもを通して動滑車のしくみにし一方のひものはしに、ばねばかりをつけて、その目もりを読みます。

すると、ばねばかりがひもをひいている力は①のときの2分の1になっていることがわかります。

これは、動滑車と重りをつるしているのは1本のひもではなくて、2本のひもであるからです。

もちろん滑車に通してあるひもは、続いている1本のひもですが動滑車の一方のはしから入って他方のはしから出ているので動滑車の両はしをあわせて1本のひもでつるしていることになるのです。

このことは、棒の真ん中に荷物をつるしふたりでその両はしを持ち上げれば、ひとりが出す力は荷物と棒の重さの、半分の力ですむということと同じです。

この場合、棒の一方のはしを人が持つかわりにひもでどこかにつるしても、同じです。

このように動滑車のしくみを使うと、ひもを引く力は滑車と重りの重さの半分でよいことになります。

これが、動滑車のはたらきです。

また、動滑車は、図のように、支点がはしにあって作用点が真ん中、力点がもう一方のはしにあるてこと考えることもできます。

このてこでは、支点から作用点までの距離は滑車の半径にあたり、支点から力点までの距離はその2倍（直径）になっています。

このことからも、力が半分でよいことがわかります。

動滑車の重さは、重りの重さにくらべるとごく小さいのがふつうですから、動滑車の重さは考えにいれないことにします。

すると、動滑車で重りを上げるとき、ひもを引く力の大きさは重りの重さの半分でよいことになります。

動滑車だけで重りを上げるには上向きにひもをひかなければならないので、たいへん不便です。

そこで、下向きに引く力で重りを上げられるように、いつも定滑車と組み合わせて使います。

てこと仕事

てこを使うと、支点から作用点までの距離と支点から力点までの距離の関係から、小さな力で大きな力がえられます。

しかし、小さな力で大きな力をえるためには、支点から力点までの距離が、支点から作用点までの距離より大きくなければなりません。

たとえば、下の図のように、支点から作用点までと支点から力点までの距離の比が、1対10のとき作用点と力点のそれぞれの点で仕事の量はいくらになっているかを考えてみましょう。

力点で、2キログラムの力をくわえ、1メートル動かしたとすれば力点がした仕事は、2（kg）× 1（m）= 2（kgm）で2キログラムメートルになります。

いっぽう、作用点では、力のモーメントから、2キログラムの10倍、すなわち20キログラムの力がはたらくことになります。

しかし、力点で1メートル動かしても、作用点では10分の1しか動きません。

したがって、作用点では、20（kg）×1/10（m）＝ 2（kgm）で2キログラムメートルの仕事をしたことになります。

ですから、てこを使っても、使わなくても仕事の量にはかわりはありません。

輪軸と仕事

輪軸を使っても、小さい力で、大きな力がえられます。
これは、小さい力でも、大きく動かせば大きな力がはたらくということです。

たとえば、下の図のように、小さい円の半径をｒメートルとして小さい半径と大きい半径の比が1対2であるような輪軸を使って仕事の原理を考えてみましょう。

1キログラムの力で、輪軸が一回転する仕事をしたとすれば仕事の量は、1（kg）× 4πr（m）= 4πr（kgm）です。

他方、1キログラムの力とつりあう力は、2倍の2キログラムです。
したがって、小さい円を一回転させるわけですから、2（kg）× 2πr(m)＝ 4πr（kgm）となります。

ですから、輪軸を使っても、使わなくても仕事の量にはかわりがありません。

このあとで学ぶ滑車や斜面の場合にも仕事の量にはかわりはなく力で得をして距離で損をしています。

仕事

私たちが、日常用いている仕事という言葉の中には私たちが物をつくったり、考えたり、書いたりする意味がふくまれています。

たとえば、距離の仕事は終わったというときに用いる“仕事”という言葉は、これに相当します。

しかし、理科で用いる仕事という言葉の意味は物体にはたらく力がする仕事という意味です。

たとえば、ある物体を手でまっすぐ持ち上げるときその物体の重さに等しい力を上向きに加えなければなりません。

このように、物体に力を加えて、その物体を力の方向にある距離だけ動かしたとき、その力は物体に仕事をしたあるいは、物体は仕事をされたと言います。

仕事のあらわし方

仕事の量をあらわすには、ある物体に加えた力の大きさとその物体に加えられた力の方向に動いた距離とをかけあわせた値であらわされます。

ですから、仕事の量を式であらわすと

（仕事の量）＝（力の大きさ）×（力の方向に動いた距離）

となります。

この式でもわかるように、物体に力がはたらしてしてもその物体が動かなかったり、あるいは、力がはたらいていないのに物体が動いているときには、仕事をしたことにはなりません。

たとえば、重い荷物をひいても、その荷物が動かなければ仕事の量は0ですから、仕事をしたことにはなりません。

仕事の量は、力の大きさと物体が力の方向に動いた距離との積であらわすので仕事の単位も、力の単位と距離の単位の積であらわします。

ある物体に、1キログラムの力がはたらいてその物体が1メートル動いたとすると、単位は、キログラムメートルで1（kg）× 1（m）= 1（kgm） となります。

また、物体に1ニュートンの力が加えられ物体が1メートル動いたとすれば、そのときした仕事の量はジュールという単位であらわされ。

仕事の量は、1ジュールということになります。

1ジュールの1千万分の1を、1エルグと言います。
そして、1キログラムメートルは約9.8ジュールにあたります。

仕事の原理

私たちが、柱に打ちこんである釘を手で抜こうとしてもなかなか抜くことができません。
しかし、釘抜きを使うと、かんたんに抜くことができます。

また、山登りをするときにも遠まわりしてでもゆるい坂を登ったほうが楽に登ることができます。

この場合、力では得をしていますが坂を登るため、距離で損をしていることになります。
また、急な坂を登るときは力では損をしていますが距離では得をしていることになります。

てこの原理を応用した道具には、たくさんあります。
まえに述べた釘抜きの場合も、力点の動く距離が大きくなるため力では得をしてしますが、距離で損をしていることになります。

このように同じ仕事のときは、力が小さければ距離が大きくなり、力が大きくなれば距離か小さくなります。

したがって、どんな機械を用いても仕事で得をすることも、損をすることもありません。

これを、仕事の原理と言います。

仕事率

同じ仕事をするにしても、1時間かかる機械と2時間かかる機械とを用いたのでは、1時間でできる機械を用いたほうが2倍も得になります。

そこで、仕事を考えるときには、一定の時間内に機械が仕事をどのくらいの速さでするかを考える必要があります。

仕事の速さに、1秒間とか1時間にする仕事の量であらわしこれを仕事率と言います。
1秒間に1ジュールの仕事をするとき1ワッ卜（W）という仕事の単位を用います。

1ワッ卜の1000倍が1キロワット（kW）です。
これは、電気のする仕事の速さをあらわす単位です。

有効率

外から機械に仕事をあたえても、それが全部役立つことはありません。

外からあたえられた仕事の一部分が使われてあとの残りは、摩擦などによって、無駄に費やされてしまうからです。

そこで、機械がする有効な仕事が外からあたえた仕事の何パーセントにあたるかを考えてこれを有効率、または、たんに効率と言います。

効率はつぎのような式であらわすことができます。

このように、仕事をする場合には効率の高い機械を用いることが、非常に重要な問題となります。

輪軸の利用

私たちの使っている道具や機械には、輪軸のはたらきを利用して小さい力で、大きな力を出すようにしたものが、たくさんあります。

自動車のハンドル・ドライバー・ラジオやテレビのつまみなどはみな軸のまわりに輪をつけたもので、輪をまわす力は小さくても軸をまわす力は、大きくなるようになっています。

しかし、輪軸のはたらきを利用した機械でも輪のかわりに、軸に長い腕をつけたものがあります。

輪がなければ、輪軸ではないと考えるのは、間違いです。

輪軸のはたらきは、てこと同じですから、輪のかわりに腕をつけてその先に力を加え、大きなモーメントを軸にあたえても、よいわけです。

腕時計のぜんまいをまく、りゅうずは輪をもった輪軸ですが柱時計や置時計のぜんまいをまくねじは、腕をつけた輪軸です。

スパナも同じように、腕を利用した輪軸です。

ナットを、指先で硬くしめつけるのは無理ですが、スパナを使って、そのはしに力をかけると、大きなモーメントになって、楽にしまります。

自転車のハンドルも、腕をつけた輪軸です。

ウィンチ

輪軸のはたらきを利用して重い物をまきあげる機械をウィンチと言います。

ウィンチでは、ハンドルが輸のはたらきをしています。
ハンドルをまわすとロープに大きな力が出て重い物でも、楽に動かすことができます。

ハンドルの力を軸に伝えるのに、歯車を組み合わせて使うと加える力がさらに小さくてすみます。

また、ハンドルをまわすのに、モーターを使うと力も大きく、仕事も早くできます。

ビルの建築工事場や、工場・港・駅などで重い物を軽々と運びあげているクレーンは、滑車のロープをこのウィンチでまきあげています。

しゃち

海辺にいくと、漁師たちが、しゃちという道具をまわして船を陸に引き上げているのを見かけます。

これも、腕をつけた、輪軸の一種です。

きり・ドライバー

きりやドライバーも、輪軸を利用したものです。

太いえのところが輪軸の輪のはたらきをし、先のところが軸のはたらきをしています。

そのため、えに加える力が小さくても、先のところに大きな力が出て大きな抵抗に打ち勝ち、穴をあけたり、ねじをまわしたりできるのです。

自転車のクランク

自転車のペダルを踏むと、クランクがまわりそれといっしょに、クランクの軸につけた大きな歯車がまわります。

この歯車の回転力は、チェーンによって後輪の歯車に伝わります。
後輪の歯車はチェーンから受けた力でまわり、その回転力を車軸に伝えます。

このように、クランクの力が後輪の車軸に伝わるまでには二度も輪軸のはたらきが利用されています。

いま、クランクとチェーンとの組み合わせを考えてみるとクランクは輪軸につけた腕にあたり、チェーンをまいた歯車は軸にあたります。

そこで、チェーンに出てくる力は、

となります。

クランクの長さが20センチ、歯車の半径が10センチとしてペダルを20キログラム重の力で踏むとするとチェーンには40キログラム重の力がでます。

鉛筆削り

鉛筆削りにも、輪軸のはたらきが、上手に利用してあります。

下の図を見てください。

ハンドルは、輪軸の輪のはたらきをしています。
ハンドルをまわすと、鉛筆を差し込むところと、刃のついた円筒が中心線ＡＢのまわりにまわります。

また、刃のついた円筒のはしには、歯車がついていて動かない枠の内側の歯車とかみあっています。

そのため、円筒は中心線ＡＢのまわりをまわりながら円筒の中心線ＣＤのまわりにもまわります。

差し込んだ鉛筆は、この円筒の刃に決まった角度で触れているので、きれいに削れるのです。

しくみが込み入っているので、ＣＤをＡＢに重なるようにずらしまた、鉛筆の位置もずらして考えてみます。

すると、刃のついた円筒が、輪軸の軸のはたらきをしていることがよくわかります。

輪軸のはたらき

太い軸に、半径の大きな輪を硬くつけていっしょに回転するようにしたものを、輪軸と言います。

2本のつなを用意して、輪軸の軸と輪にそれぞれ反対向きにまきつけてみます。

そして、軸にまいた綱のはしに、重い物体を結びつけておきます。

輪にまいた綱をひいて、輪軸をまわすと軸の綱は、だんだん軸にまきとられて、そのはしに結んだ物体を引き寄せていきます。

このとき、輪にまいた綱を引く力は物体が重くても、小さくてすみます。

輪軸は、このように、大きな輪をまわすことによって軸に大きな力をださせるはたらきをします。

輪軸のつりあいの実験

輪と軸の半径が、2対1、3対2になっている2つの輪軸と重さの等しい重りをたくさん用意します。

そして、1つの輪軸の軸にまいた綱に、いくつかの重りをつるしておいて、輪にまいた綱に、重りを何個つるしたらつり合うか、調べてみます。

つぎに、軸の綱の重りをかえて、輪の綱の重りの数がいくつのときつり合うかを調べます。
別の輪軸についても、同じような実験をします。

表は、この実験をまとめてみたものです。
この表から、つぎのような関係が成り立っていることがわかります。

「輪軸がつり合っているときには軸の半径に軸につるした重りの数をかけた数は輪の半径に輪につるした重りの数をかけた数にいつも等しくなっている」

重りの数は、重りが綱を引いている力、つまり、綱が輪や軸をまわそうとして綱が輪や軸にふれているところにはたらいている力の大きさをあらわしています。

ですから、輪や軸の半径に重りの数をかけたものは輪軸の中心のまわりの力のモーメントをあらわしてにいることがわかります。

そして、この2つの力のモーメントは、反対まわりになっていますから、モーメントの大きさが等しいと、輪軸はつり合うことになります。

輪軸のつり合いは、つぎのような式であらわすことができます。

r×P = R×Q

ｒ……軸の半径
P……重りが軸の綱を引く力
R……輪の半径
Q……重りが輪の綱を引く力

輪軸とてこ

輸軸とてこをくらべてみると、そのはたらきが非常によく似ていることがわかります。

輪軸の中心は動かないようにとめてありますから、てこの支点にあたります。

物体の力は、綱が軸にふれているところにかかりますからここがてこの作用点にあたります。

また、輪につながれているところに手で綱を引く力がはたらきますから、ここは、てこの力点にあたります。

したがって輪軸は、てこのはたらきと同じになります。
そこで、輪軸のつり合いをあらわす式は、当然てこの原理と一致します。

まえの式を書きかえると、

となります。
この式からわかるように、輪の半径が大きいほど軸の半径が小さいほど小さい力で、重い物体を動かすことができるわけです。

てこの利用

私たちが使っている道具や機械のうちにはてこのはたらきを利用したものが、たくさんあります。

しかし、てこのはたらきは、支点の位置によってかわりますからわけて調べてみましょう。

支点がなかにあるてこ

まくらになる丸太を使って、棒で大きな石を持ち上げるときには手で棒を押し下げるところが力点、石にあたっている棒のはしが作用点、まくらのところが支点になっています。

この場合、まくらを石に近づけるほどまた、押すところが棒のはしに近いほど、大きな力がでます。

このように、支点と作用点のあいだを短く支点と力点のあいだを長くすると、小さい力で大きな力がでます。

このようなてこを、第一種のてこと言います。

紀元前三世紀に、ギリシアの有名な学者アルキメデスは「我に支点をあたえよ。そうすれば、地球をも動かしてみせる」と言ったと伝えられています。

これは、第一種のてこのはたらきを、よくあらわしています。
地球の外のどこかに、支点をつくれるなら地球のような重いものでも、動かせるわけです。

かじや・ポンプのえ・ペンチ・釘抜き・洋ばさみなどはこの第一種のてこを利用したものです。

かじやは、先の近くが曲がっていて、ここが支点になります。
釘をはさむ先のところが作用点です。

このため、まっすぐな長いえのはしに力をかけると作用点に大きな力がでて、釘が楽に抜けるのです。

洋ばさみは、支点がいっしょになっている、2つのてこの組み合わせです。

指を入れて、力を加えるところと支点との距離は決まっていますからなるべく支点の近くに物をはさむようにすると大きな力がでて、厚い紙でもよく切れます。

支点がはしにあるてこ

まくらを使わないで、棒で重い石を動かすときには、棒の先を地面につけ、その近くに石をあてておいて、棒の手もとのはしを押し上げるようにします。

このように、支点が棒のはしにあって、作用点が力点と支点とのあいだにあるてこを、第二種のてこと言います。

このときも、作用点が支点に近いほど、力点が支点から遠いほどてこの出す力は大きくなります。

紙をきるカッター・缶切り・栓抜きなどはこの種類のてこのはたらきを利用したものです。

ボートをこぐオールはその先が水中に止まっていて支点のはたらきをしています。

そのため、オールの手もとをひくと止め輪のところ（作用点）に大きな力が出て、ボートを押し進めます。

オールの先が動いているように見えるのは動いているボートの上から見ているからです。
ですからボートの上から見れば、止め輪を支点と考えてもよいのです。

支点がはしにあっても、第二種のてこと違って力点が作用点よりも、支点に近くなっているてこがあります。

これを第三種のてこと言います。

このてこでは、作用点に出る力は力点に加える力より小さくなるので、力ではそんをします。

そのかわり、力点の小さな動きを作用点の大きな動きにかえるはたらきをします。

ピンセット・毛抜き・日本ばさみなどは、このはたらきを利用したものです。

私たちのうでも、第三種のてこになっています。
ひじのところか支点になっていて筋肉が少し縮むだけで手は大きく動きます。

なお、第一種のてこでも、支点と作用点との距離が支点と力点との距離より大きいときには力のとくはできません。

しかし、作用点の動きを、大きくすることができます。

---

---

てんびん

金属の棒の中央を支えて支点とし、支点から同じ距離のところに同じ重さのさらをつるしたはかりが、てんびんです。

てんびんで重さを測るには、左側の皿に、測ろうとする物を載せます。
右側の皿には、分銅を適当に載せて、棒が水平になるようにします。

それには棒の中央から、長い針が下向きにつけてありますからその先が目もりの中央で止まるようにすればよいのです。

支点から、皿をつるしてあるところまでの距離は左右等しくしてありますから、てんびんがつりあったときには分銅の重さと物体の重さは、等しいはずです。

したがって、分銅が何グラムのっているかを調べるとさらに載せてある物体の重さ（正確に言えば物体の質量）がわかります。

分銅は、100グラムから1000分の1グラムまでいろいろの質量のものを1組として、箱に入れてあるのがよく使われます。

1つ1つの分銅は、それに刻んである数字に正しく質量があうようにつくってあります。

ですから、分銅を扱うときは、手で握って錆びさせたりしないように備え付けのピンセットではさみます。

また、小さい分銅は、なくなりやすいから、よく注意しなければなりません。

てんびんの感度

重さを、できるだけくわしく測るには、ごくわずかの重さの違いでもてんびんの棒が、大きく傾くようになっていればよいわけです。

それには、てんびんの両腕（てんびんの棒で、支点を中心にしてその左半分を左腕、右半分を右腕という）の重さができるだけ軽く、腕の長さが、長いほどよいのです。

また、金属棒と支点とのあいだの摩擦をできるだけ小さくしなければなりません。

そこで、硬い物質を、ナイフの刃のようにとがらせたものを棒の中央の下側にとりつけ、これを硬い台の上にのせて棒を支えるような工夫がしてあります。

非常に感度のよいてんびんでは1グラムの百万分の1ぐらいまで、正確に測れるものがあります。

上皿てんびんの使い方

いろいろのてんびんのうちで、もっともかんたんなてんびんが、上皿てんびんです。

これは、その名前の通り、皿が両腕のはしに上向きに載せてありますから、物体や分銅を載せたり降ろしたりするのが、とても楽です。

上皿てんびんにも、いくつかの種類がありますがふつうは、10分の1グラムぐらいのくわしさで100グラムまたは200グラムまで測れるものが、よく使われています。

上皿てんびんを使って、重さを測るにはまず、てんびんを水平の面に置くことが大切です。

てんびんが水平かどうかを調べるには、さらに何も載せていないときてんびんについている針が、目もりの真ん中きているかどうかを調べます。

もし、傾いているときは横についているねじをまわして、直します。

つぎに、皿の上に紙を載せ、測ろうとする物体を左の皿に載せ、右の皿に、分銅を載せていきます。
測ろうとする物体も、分銅も、皿の上に直に載せてはいけません。

分銅の載せ方は、つぎの例のようにします。

てんびんのさらに、63グラムの物体が載っているとします。
もちろん、はじめには、何グラムかわかっていません。

まず、だいたいの検討で、100グラムの分銅を静かに載せてみますと分銅の皿が下がって、重すぎることがわかります。
そこで、100グラムの分銅をおろして50グラムの分銅を載せてみます。
こんどは、分銅が足りないことがわかります。

このことから、物体の重さは100グラムと50グラムのあいだであることが、わかりますから、つぎに、20グラムの分銅を載せてみます。

これでは、重すぎることがわかりますから、10グラムにかえてみます。
すると今度は、軽過ぎます。

そこで、物体の重さは70グラムと60グラムのあいだであることがわかります。

このように、はじめに大きい分銅を使ってだいたいの範囲を探します。
つぎに、これより小さい分銅を使って、この範囲をだんだんせばめていけば、ついにはつり合うようになって重さがわかります。

薬品のようなものを、ある分量だけ測りとりたいときにははじめに、その重さにあたるだけの分銅を、左の皿にのせておきます。

それから、右の皿に、さじを使って、少しずつ薬品を載せていきてんびんがつり合うようにします。

分銅の載せ降ろしは、ピンセットを使って、静かにします。
皿から降ろした分銅は、そのつど箱の中にもどします。

竿秤

竿秤は、目もりをつけた棒（竿）のはしに皿をつるしそこから少しはなれたところに、さげをつけたものです。

竿には、ひものついた重り（分銅）をかけて自由に動かせるようにしてあります。

竿秤で重さを測るには測ろうとする物をさらにのせてさげおを持ってつるします。
分銅を動かして、竿が水平になったとき分銅のひものあるところの目もりを読めばよいのです。

このはたらきは、てこのつりあいにあたるわけでさげおの位置が支点、分銅のひもの位置が力点、皿をつるしてあるはしが作用点になっています。

竿秤のつくり方

太さがいちようで、長さが30センチぐらいの、まっすぐな棒を竿にします。
小さい缶のふたにひもをつけ、これを竿につるして、皿にします。

さげおは、皿をつけたはしから5センチぐらいはなれたところに上向きにつけます。

分銅には、小石とかガラス玉を何個か布きれに包んでこれにひもをつけて使います。

これで材料がそろったので、こんどは竿に目もりをつけなければなりません。

まず、さらに何ものせないで、さげおをもってつるし竿が水平になるように、分銅を動かします。

竿が水平になったら、このときの分銅のひもの位置に0（グラム）の目もりをつけます。

つぎに、皿の上に、本当の分銅10グラムをのせて竿が水平になるように、重りの分銅を動かします。
このときは、ひもの位置に10（グラム）の目もりをつけます。

さらに、本当の分銅20グラム・30グラム……を使って同じようにして、20・30……の目もりをつけます。

これで、大きい目もりをすませました。
0・10・20・30……の目もりのそれぞれの間隔は同じになっているはずです。

そこで、0と10、10と20……のあいだを10等分して小さい目もりをつけます。
これで、竿秤ができあがりました。

竿秤をつくるとき、200グラムまで測れるようにしたいと思っていたのに、実際につくってみると、50グラムしか目もりがつけられなかったというようなときは、どうしたらよいでしょうか。

それには、てこの原理を考えれば、すぐわかります。
さげおの位置をもっとはしによせるか、重りの分銅をもっと重くすればよいのです。

そのかわり、目もりは、すっかりやり直さなければなりません。

本当の竿秤では、2本のさげおが違った位置につけてありそれぞれの目もりを、竿の両面に印してあります。

重りの分銅は、決まったものを、1つ使います。

竿秤の感度　

本当の竿秤につけてある、2通りの目もりをよく注意してみると軽い範囲しか測れないほうの目もりは、その間隔が長くなっています。

このことは、ごくわずかの重さの違いでも分銅を大きく動かさねばならないことつまり、竿が傾きやすいことを意味しています。

したがって、わずかの重さの違いでも、測りやすくなっているのです。
これを「測りの感度がよい」と言います。

竿秤の感度は、さげおの位置をさらをつるしてあるはしから遠くはなすほどまた、重りの分銅が軽いほど、よくなります。

しかし、感度をよくすれば測ることのできる最大の重さは小さくなります。

力のモーメント

てこのつりあいの実験を、もういちど考えてみましょう。

左側の重りは力Ｐで棒を下に引いていますから、支点のまわりに棒を左まわり（時計の針の回転と反対まわり）にまわそうとしています。

また、右側の重りは力Ｑで棒を下に引いていますから棒を右まわりにまわそうとしています。

この2つのはたらきが、ちょうど等しくなっているのでてこは水平につりあっている、と考えることができます。

したがって前の式は、このはたらきをあらわしていることになります。

つまり、a×Pは、力Ｐが、棒を支点のまわりに左まわりにまわそうとするはたらきをあらわしb×Qは力Ｑが棒を支点のまわりに右まわりにまわそうとするはたらきをあらわしています。

いっぱんに、物体に力Ｆがはたらいて、物体の中のある点Ｏのまわりに物体をまわそうとするとき、そのはたらきの大きさのことをＯのまわりの力Ｆのモーメントと言います。

そして力のモーメントは
（Ｏと力点との距離）×（力の大きさ）であらわされます。

したがって、a×Pは支点のまわりの力Ｐのモーメントb×Qは支点のまわりの力Ｑのモーメントをあらわしています。

そして、力Ｐのモーメントは左まわり力Ｑのモーメントは右まわりであって、その大きさが等しいのでつりあっていると言えます。

力のモーメントは力が大きいほどまた、カ点が支点からはなれているほど大きくなります。

スパナでナッ卜をまわすときなるべくスパナのはしをもってまわすと楽にまわすことができます。

また、ドアを開けたり閉めたりするとき蝶番のすぐそばを押しても、なかなか動きません。
しかし、とってのところを押すと、同じ大きさの力でも楽に動きます。

それは、力点が支点からはなれているので力のモーメントが大きくなるからです。

これまでのことは力の向きが支点と力点とをむすぶ直線に垂直になっている場合でした。
しかし、力の向きがてこに垂直になってしないときは同じ大きさの力が同じところにはたらいても、力のモーメントは小さくなります。

下の図のような向きに、力がはたらいている場合、力Ｆを、スパナに垂直な分力と、平行な分力とに分解してみます。

スパナに平行な分力は、スパナを回転させるはたらきをしていません。
スパナを回転させようとする力は、垂直な分力だけです。
この力は力Ｆより小さいので、力のモーメントも小さくなります。

力を分解して考えるかわりに、力のはたらいている方向（ＡＢ）に支点から垂線をおろし、その長さを力点と支点との距離（l’）にして考えてもよいのです。

この方法でもとめた力のモーメントは力を分解した場合と同じになります。