斜面の力をもとめる方法
まえの実験からでは、摩擦があるので正しい力の大きさをもとめることはできません。
そこで、斜面にそって落ちる力を正しくもとめる方法を考えてみましょう。
斜面の力をもとめる方法には、図を書いてもとめる方法と計算でもとめる方法の2通りがあります。
図を書いてもとめる方法
この方法は、力の大きさをあらわすのに矢印を使い、矢印の方向は力がはたらいている方向とします。
矢印の長さは、力の大きさの割合をあらわすように書きますたとえば、1キログラムを1センチの長さであらわしたとすると5センチの矢印は、5キログラムをあらわすものとします。
下の図のように、斜面の傾きを30度として斜面の上に3キログラムの物体を載せます。
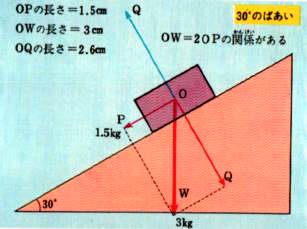
この場合、物体にはたらく重力のWは、真下に向かってはたらきます。
このとき、0Wの力は、斜面にそって落ちようとする力OPと物体が斜面に垂直におさえつける力OQの2つの力に分解されます。
このOQという力の反作用として、抗力OQ’がはたらいています。
重力OWを対角線としOPとOQの力を二辺とする平行四辺形をつくってみます。
OWの長さとOPとOQの長さを測ると力の大きさの割合がもとめられます。
たとえば、上の図で斜面の上に3キログラムの物体の重力OWを3センチであらわしたとするとOPの力の大きさは、15センチであらわされます。
また、45度の斜面の上の物体は下の図のように30度の斜面の上の物体よりも滑りやすくなります。
これは、30度の斜面の上においた物体と同じ重さの物体を45度の斜面の上に置いてみるとわかります。
つまり、30度のときのOPと45度のときのOPとでは45度のときのOPのほうが大きいのです。
計算でもとめる方法
OPの力は、計算によっても、もとめることができます。
物体の重さの中心をOとして、まえと同じような図を書いてみましょう。
重力OWの矢印と、斜面にそって落ちようとする力OPの矢印と出てきた三角形OWPをもとの三角形ABCとくらべてみましょう。
この2つの三角形では、角Bと角Wが30度、角Aと角Oが60度、角Cと角Pが直角でそれぞれ等しくなっています。
この2つの三角形は、3つの辺の長さの割合が同じになります。
つまり、OWの力とOPの力の大きさの割合は斜面をつくっている三角形ABCの、傾いた辺の長さ(AB)と垂直の辺の長さ(AC)との割合に等しくなります。
これを比例式であらわすと 〇W : OP = AB : AC となります。
これを変形すると OP=OW × AC/AB となります。
たとえば、30度の傾きをもった斜面ではABの長さと、ACの長さの割合は、2対1です。
いま、この斜面に3キログラムの物体をのせると OP= 3(kg) × 1/2 = 1.5(kg) となりまえと同じく、1.5キログラムになります。
傾いた辺の長さと、垂直の辺の長さを測って、その割合をもとめておくと、OWがどのような値でも、OPがもとめられます。
斜面と仕事
斜面を使って、物体を引き上げたときにする仕事もてこや滑車・輪軸を使ったときにする仕事と、原理は同じです。
つまり、力では得をしていますが、距離で損をしています。
たとえば、4キログラムの物体を人の手で1メートル持ち上げたときにした仕事の量は 4(kg)× 1(m)= 4(kgm) となります。
これを30度の斜面で引き上げたときの仕事を考えてみましょう。
斜面の上に4キログラムの物体を落ちないように支えるには、上の公式から Pの力 = 4(kg) × 1/2 = 2(kg) で、つまり、2キログラムの力で反対の向きにくわえればちょうどつり合うことになります。
30度の斜面の距離は、高さの2倍の距離がありますから1メートル上げるには、斜面の上を、2メートル動かさなければなりません。
ですから、30度の斜面で、物体を1メートル引き上げたときの仕事の量は、 2(kg)× 2(m)= 4(kgm)となります。
したがって斜面を使わないで、物体を持ち上げるときにする仕事も斜面を使って、それと同じ高さまで物体を引き上げるときにする仕事も仕事の量としては、かわりがありません。
しかし、実際には、斜面を使った場合には斜面と物体とのあいだで、摩擦がはたらいているのでその分だけ余計に力が必要です。
図は、物体の重さが一定なときに、斜面の角度をかえることによって引き上げるときの力の大きさの違いを、矢印であらしわしたものです。