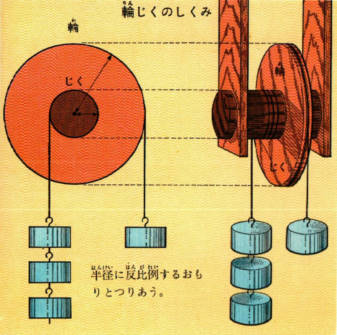
輪軸のはたらき
太い軸に、半径の大きな輪を硬くつけていっしょに回転するようにしたものを、輪軸と言います。
2本のつなを用意して、輪軸の軸と輪にそれぞれ反対向きにまきつけてみます。
そして、軸にまいた綱のはしに、重い物体を結びつけておきます。
輪にまいた綱をひいて、輪軸をまわすと軸の綱は、だんだん軸にまきとられて、そのはしに結んだ物体を引き寄せていきます。
このとき、輪にまいた綱を引く力は物体が重くても、小さくてすみます。
輪軸は、このように、大きな輪をまわすことによって軸に大きな力をださせるはたらきをします。
輪軸のつりあいの実験
輪と軸の半径が、2対1、3対2になっている2つの輪軸と重さの等しい重りをたくさん用意します。
そして、1つの輪軸の軸にまいた綱に、いくつかの重りをつるしておいて、輪にまいた綱に、重りを何個つるしたらつり合うか、調べてみます。
つぎに、軸の綱の重りをかえて、輪の綱の重りの数がいくつのときつり合うかを調べます。
別の輪軸についても、同じような実験をします。
表は、この実験をまとめてみたものです。
この表から、つぎのような関係が成り立っていることがわかります。
「輪軸がつり合っているときには軸の半径に軸につるした重りの数をかけた数は輪の半径に輪につるした重りの数をかけた数にいつも等しくなっている」
重りの数は、重りが綱を引いている力、つまり、綱が輪や軸をまわそうとして綱が輪や軸にふれているところにはたらいている力の大きさをあらわしています。
ですから、輪や軸の半径に重りの数をかけたものは輪軸の中心のまわりの力のモーメントをあらわしてにいることがわかります。
そして、この2つの力のモーメントは、反対まわりになっていますから、モーメントの大きさが等しいと、輪軸はつり合うことになります。
輪軸のつり合いは、つぎのような式であらわすことができます。
r×P = R×Q
r……軸の半径
P……重りが軸の綱を引く力
R……輪の半径
Q……重りが輪の綱を引く力
輪軸とてこ
輸軸とてこをくらべてみると、そのはたらきが非常によく似ていることがわかります。
輪軸の中心は動かないようにとめてありますから、てこの支点にあたります。
物体の力は、綱が軸にふれているところにかかりますからここがてこの作用点にあたります。
また、輪につながれているところに手で綱を引く力がはたらきますから、ここは、てこの力点にあたります。
したがって輪軸は、てこのはたらきと同じになります。
そこで、輪軸のつり合いをあらわす式は、当然てこの原理と一致します。
まえの式を書きかえると、
となります。
この式からわかるように、輪の半径が大きいほど軸の半径が小さいほど小さい力で、重い物体を動かすことができるわけです。