速さと速度
人が道を歩いたり、自転車で走ったりするときとかまた、ヘリコプターと自動車とどちらがどのくらい速いかというようなときに速いか遅いかを含めるには、速さという言葉の意味を含めないとはっきりしたことがあらわせません。
そこで1時間とか1秒間に、どれだけの距離を動いたかで、その速さを含めています。
たとえば、人が1時間に4キロメートル歩いたとすればその速さは毎時4キロメートルと言いあらわします。
また、小銃のたまが、1秒間に600メートル飛んだとすればその速さは、毎秒600メートルであると言います。
このように速さは、一定の時間内に、物体の動いた距離であらわせばよいのです。
その単位には、距離と時間の単位をならべて、毎時何キロメートル、あるいは何キロメートル毎時(km/時)というように、あらわすことになっています。
100メートルを、12.5秒で走る人の速さは、毎秒 100/12.5 = 8なります。
この場合、はじめと中ほどと終わりのころとでは、速さが違うかもしれません。
したがって、毎秒8メートルという速さは、この人の平均の速さを意味しています。
同じ速さで動いても、東へ動くか、北へ動くか、その物体の動く方向によって位置のかわり方は、まったく違います。
たとえば、図で、一点Oから同じ速さで動きはじめても東へ迎えばA点にくるし、北へ迎えばB点にきます。
そこで、物体の速さとあわせて方向もつけ加えると物体の動きが非常にはっきりします。
このように、方向も合わせて速さをあらわすときは、速度と言います。
速度をあらわすときは、矢印を使います。
矢の長さで速さをあらわし、矢の向きでその方向をあらわせば、はっきりします。
速度の大きさの単位も、メートル毎秒(m/秒)と言うようにあらわします。
速度の合成と分解
流れの速い川を泳いでわたるときは川の流れと直角に泳いでいても少しずつ流されていきます。
このときは、泳ぐ速さと流れの速さとから、体の進む方向を決めることができます。
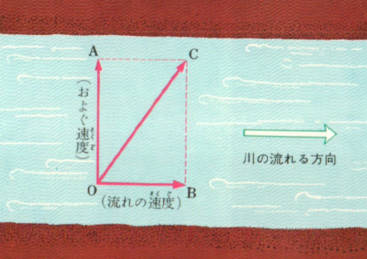
図のように、泳ぐ速度と流れの速度に比例する長さで矢印OAとOBを書き
これが二辺となるような平行四辺形を書きます。
その対角線OCをもとめると、これが泳いでいる人の進む方向と、速さになります。
たとえば、泳ぐ速さが毎分4メートル、流れの速さが毎分3メートルであれば紙の上にOAを4センチ、OBを3センチにして、平行四辺形を書いてみます。
OCをものさしで測ってみると、約5センチとなります。
したがって、体の進む速さは、毎分5メートル、その方向はOCとなるにわけです。
このように、平行四辺形を使って、2つの速度からこれが合わさったときの速度をもとめることを速度の合成と言います。
この方法は、力の合成の平行四辺形法とまったく同じで力や速度などのように、大きさと方向のある量には、すべてあてはまります。
また、まえの例のOAとOBとが、直角でなくて、どんな角度でも成り立ちます。
つぎに、OCがわかっていて、これをもとにして、泳ぐ速度OAと流れの速度OBをもとめることを速度の分解と言います。
1つの直線OCを対角線にもつ平行四辺形は、いくつもあります。
したがって、ある速度を分解するには、分解する2つの速度の方向がわかっているか、1つの速度の大きさと方向がわかっているときだけ、決まった答えがでます。
直線運動・曲線運動
まっすぐなレールの上を、電車や汽車が走るときのように動く方向が直線である運動を直線運動と言います。
このとき、速さが一定であれば、等速直線運動と言います。
これに対して。高く打ち上げた野球のボールのように曲がった道筋を通る運動を曲線運動と言います。
曲線運動では、速さが一定であっても方向がいつもかわりますから、速度は絶えずかわっています。