流れに対してななめにおいた板
川の流れや空気の流れの中に、流れに平行に板をおくと板は流れからそれほど力を受けません。
ところが、流れに対してななめに板をおくと流れの方向に押し流されようとしますが板の面に、垂直の力を受けます。
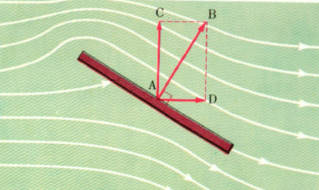
図のように、水の流れに対して、ななめに板をおいた場合を考えてみましょう。
板の面には、垂直に力がかかるので、板にはABという力がはたらきます。
この力を平行四辺形の法則によって流れの方向の力ADとADと直角の方向のACという力に分解してみます。
ADの力は、水の流れの方向ですから、板を押し流すようにはたらきます。
それから、ACは、板を上のほうに持ち上げるようにはたらきます。
ABは、流れが速いほど、また、板が流れに対して直角に近いほど大きくなりますが、板が、流れに対して45度以上になると、ACの力は小さくなります。
船のかじや、飛行機の主翼やかじにはたらく力も、これと同じことが言えます。
飛行機の翼にはたらく力
グライダーでも飛行機でも、重さがありますからこの重さをどのように支えて空中に浮かばせるかということが、まず問題です。
飛行機を、空中に浮かばせるはたらきをするのは、主翼です。
主翼は、風が下からあたるように、まえが少し高く取り付けてあります。
この主翼の傾きを、迎え角と言います。
むかえ角をつけた主翼に、風があたるときは、ちょうど、水の流れに対してななめにおいた板と、同じように力がはたらきます。
たとえば、左の図①で、空気の流れの方向をGAとすると主翼にはGBという力がはたらきます。
そしてこの力は、空気の流れの方向の力GAと空気の流れに直角な方向の力GCとに分解することができます。
このGCという力が、飛行機が浮き上がる力としてはたらきます。
この力と飛行機の重さがつりあうと、飛行機は空中に浮かんでいることができます。
したがって、飛行機が浮きたがる力が飛行機の重さより大きいとしだいに飛行機は浮き上がり、反対に、飛行機の重さより小さいと下がっていきます。
また、飛行機が浮き上がるために主翼が、つぎのようなはたらきをすることも大切です。
主製の断面は、上の図の②のように、上側のまるみが大きくしてあります。
このため、主翼につきあたった空気は主翼のまえのふちで上と下の2つにわけられます。
このとき、上の空気の流れは、下の空気の流れよりも速くなります。
すると、流れが速いほど、まわりが受ける圧力は小さくなるので主翼の上側の空気の圧力が減り、下側の空気の圧力が増えてきます。
その結果、主翼の上と下とでは、圧力の差ができます。
そのため、主翼を上に持ち上げようとする力がはたらきます。
この作用は、飛行機の速さが大きいほど、大きくなります。
このことを、つぎの実験で確かめてみましょう。
実験1
スプーンを指先で軽く持ちその裏側を水道の水の流れに触れさせます。
すると、スプーンは流れに吸い寄せられて、はなれにくくなります。
スプーンの裏側は、ふくらんでいますからスプーンにそって流れる水は、この部分が速さを増します。
このため、水の圧力が減り、スプーンが水の流に吸いよせられるのです。
実験2
2枚の紙を、上の写真のようにならべてたらし、そのあいだを強く吹いてみます。
すると、2枚の紙は、互いに吸いつくようになります。
これは、紙のあいだを空気が速く流れるため内側で紙を押す空気の圧力が外側の圧力より小さくなるからです。
水や空気のようなものに、このように速さが増すと圧力が減るという性質があります。
実験3
画用紙で、図のように、翼と同じような形をつくります。
これに、きっちりと麦わらをはめこみ、麦わらに針金を通して台の上に立てます。
できあがったら、うちわで、まえから風を送ってみます。
すると、画用紙はどんどん上に上がっていきます。
これも、まえの実験と同じ原理です。翼の上面の空気の速さが増して圧力が下がり、下側の空気の速さが減って圧力が増えたため上に押し上げられるのです。