万有引力
ニュートンは、運動の3つの法則を使って、いろいろの力の問題を説きましたがその中でいちばん有名なのは万有引力の発見です。
ニュートンよりまえに、ドイツにケプラーという学者がいて17世紀のはじめに惑星(水星・金屋・火星など)の運動について3つの法則を発見していました。
その法則とは、つぎのようなものです。
第一法則
水星や金星などの惑星は太陽を1つの焦点に持つような楕円の軌道を描いて運動している。
第二法則
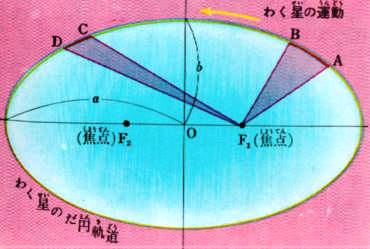
上の図で、F1に太陽があるとして、同じ時間にAからB、またはCからDまで惑星が動いたとすれば、赤線で囲んである扇形の面積が等しくなるように運動する。
第三法則
楕円には、長いほうの半径aと短いほうの半径bがあるが惑星が軌道を1周する時間(周期)の2乗は長いほうの半径の3乗に比例する。
ニュートンは、自分の立てた運動の3つの法則をもとにしてケプラーの惑星の運動の三法則を調べ、もし、太陽と惑星のあいだにつぎのような万有引力があればケプラーの法則は計算から導き出せることを発見しました。
ニュートンの考えた万有引力とは「太陽と惑星の質量の積に比例し、距離の2乗に反比例する」というものです。
これを万有引力の法則と言います。
ここで大切なことは、万有引力は質量と質量のあいだの引力で太陽と惑星とのあいだだけではなく地球上にあるすべての物体(万有)のあいだでもはたらいているということです。
磁石と磁石のあいだの磁気力、電気と電気のあいだの電気力にもこれとにたような関係があります。
このことは、18世紀の末に、フランスのクーロンという学者が万有引力の法則にヒントを得て発見しました。
重力
地球上のすべての物体は、地球の自転のために、円運動をしています。
円運動をしている物体には、それを円の中心にむかって引く力(向心力)とそれと同じ大きさで、向きが反対の力(遠心力)が、はたらいています。
重力というのは、この遠心力と物体が地球の中心に引かれる力(引力)との合力を言います。
私たちが、手で物を支えたり、ぶらさげたりすると重さを感じますがこの物体の重さとして感じるのが、重力と呼ばれるものです。
遠心力の大きさは、地球の引力とくらべると、ごく小さいものですが地球上でも赤道付近と、北極や南極のように緯度の違うところでくらべてみると、わずかながら差がでてきます。
これは、地球が自転をしているため、地球上の緯度で、地軸を自転軸として大きく円運動をするところと、全く円運動をしないところが出てくるためです。
したがって、全く円運動をしないところ(北極や南極付近)では、遠心力が生じないので重力が大きくなります。
逆に、大きく円運動をするところ(赤道)では、地球上で遠心力が一番大きいところなのでそれだけ重力は小さくなります。
そのため、重力の大きさは、赤道付近が小さく、北極や南極に近づくほど大きくなっています。
地球上で、場所によって重力が違うのはこのように地球の形や地球の自転の影響を受けているからです。
しかし、その違いはごくわずかなために地球の引力そのものを、重力と言うこともあります。
引力の大きさは、地球の中心からの距離の2乗に反比例しますから高いところへもっていくと、物体の重さは軽くなります。
たとえば、同じ物体の重さを東京と富士山の頂上とで測ると富士山の頂上のほうが、軽くなります。
さらに、地球からはなれて、月の引力と地球の引力とが同じところでは物体の重力がなくなり(無重力状態)すべての物体が空中に浮かんでしまいます。
重力の加速度は、ふりこを使って測ります。
その大きさは緯度45度の海面上で、約毎秒・毎秒980センチ(980cm/秒2)です。
赤道では978、極付近では、983ぐらいで、その差は約毎秒・毎秒5センチぐらいです。
月の世界での物体の重さは、月の引力によります。
月は地球にくらべると、質量は約82分の1、半径は約4分の1ですから、計算すると、月の世界での引力は、地球の約6分の1になります。
したがって、地球上の物体を月の世界へもっていくと、約6分の1の重さになります。