虫眼鏡
1枚の凸レンズに、えをつけて、見やすくした物が、虫眼鏡です。
細かくてみにくい物を、大きく拡大して見やすくするのに使います。
虫眼鏡の像
凸レンズでも、物とレンズとの距離が、焦点より短いときは実像ができなくて、虚像となります。
ですから、実物より大きくて、正立虚像となります。
明視の距離
目は、あまり近くの物を見ることはできません。
目が疲れないで、いちばんはっきり見ることができる距離を明視の距離と言います。
これは、ふつう25センチくらいですから虫眼鏡でも像を目から25センチくらいにつくります。
このためには、見ようとする物をレンズの焦点から、少し内側におきます。
虫眼鏡の倍率
虫眼鏡を通してみる像の大きさが実物の何倍かという数を、虫眼鏡の倍率と言います。
虫眼鏡のレンズの焦点距離をFセンチ、明視の距離を25センチとします。
目をできるだけ虫眼鏡に近づけてみたときの倍率は、つぎのような式であらわされます。

また、目をレンズの焦点においてみたきの倍率は、
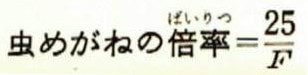
ふつう、かんたんですから、あとの式を使って計算しています。
したがって、焦点距離が小さいほど、大きな倍率がえられます。
しかし焦点距離があまり小さいとレンズは強くふくらんだ形となり、よい像ができません。
虫眼鏡は、ふつう10倍くらいまでです。
実験
虫眼鏡の倍率を、つぎのようにして、測ってみましょう。
2本のものさしを用意して、図のように下のものさしが明視の距離(25センチ)になるようにします。
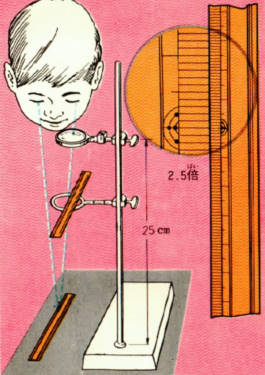
2本のものさしのめもりを、むかいあわせて平行におきます。下のものさしを右の目で見ます。
上のものさしは、虫眼鏡を通して左の目で見ながら、上下に動かします。
そして、上のものさしのめもりのはしと、下のめもりのはしが同じところに重なって見えるようにします。
ここで上のものさしの像1センチの長さにたいして下のものさしの長さが何センチになるかを読みます。
たとえば、上のものさしの1センチが、下のものさしでは2.5センチならこの虫眼鏡の倍率は、2.5倍となります。
虫眼鏡の収差
レンズによってできる像が完全でないことを、レンズの収差と言います。
虫眼鏡によってできる像もよく注意して見るといろいろ欠点を持っていることがわかります。
方眼紙を焦点距離の短い虫眼鏡で見てみましょう。
方眼紙の線は、まっすぐですが、虫眼鏡を通してみるとふちのほうはゆがんで、糸巻きのような形に見えます。
これは、ゆがみといわれる収差の一種です。
つぎに、下の写真は、凸レンズの焦点の内側にスクリーンをおき凸レンズに太陽光線をあてたときに見られる像です。
これは、色収差とよばれるものです。

光の色によって屈折率が違うため、像の大きさも違います。
そのため、完全に像が重ならず、少しずれているため色づいて見えるのです。
このほか、レンズの収差には、球面収差・こま・非点収差・曲がりなどがありこれらの収差を取り除くのは、なかなか難しいことです。


