力のモーメント
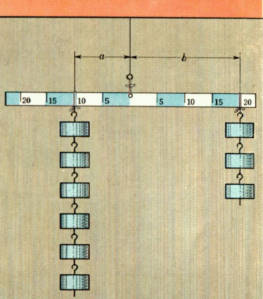
てこのつりあいの実験を、もういちど考えてみましょう。
左側の重りは力Pで棒を下に引いていますから、支点のまわりに棒を左まわり(時計の針の回転と反対まわり)にまわそうとしています。
また、右側の重りは力Qで棒を下に引いていますから棒を右まわりにまわそうとしています。
この2つのはたらきが、ちょうど等しくなっているのでてこは水平につりあっている、と考えることができます。
したがって前の式は、このはたらきをあらわしていることになります。
つまり、a×Pは、力Pが、棒を支点のまわりに左まわりにまわそうとするはたらきをあらわしb×Qは力Qが棒を支点のまわりに右まわりにまわそうとするはたらきをあらわしています。
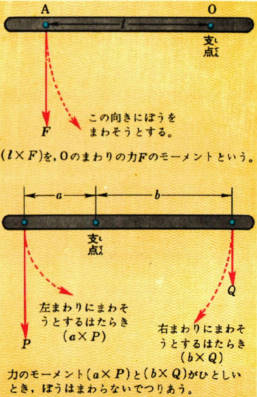
いっぱんに、物体に力Fがはたらいて、物体の中のある点Oのまわりに物体をまわそうとするとき、そのはたらきの大きさのことをOのまわりの力Fのモーメントと言います。
そして力のモーメントは
(Oと力点との距離)×(力の大きさ)であらわされます。
したがって、a×Pは支点のまわりの力Pのモーメントb×Qは支点のまわりの力Qのモーメントをあらわしています。
そして、力Pのモーメントは左まわり力Qのモーメントは右まわりであって、その大きさが等しいのでつりあっていると言えます。
力のモーメントは力が大きいほどまた、カ点が支点からはなれているほど大きくなります。
スパナでナッ卜をまわすときなるべくスパナのはしをもってまわすと楽にまわすことができます。
また、ドアを開けたり閉めたりするとき蝶番のすぐそばを押しても、なかなか動きません。
しかし、とってのところを押すと、同じ大きさの力でも楽に動きます。
それは、力点が支点からはなれているので力のモーメントが大きくなるからです。
これまでのことは力の向きが支点と力点とをむすぶ直線に垂直になっている場合でした。
しかし、力の向きがてこに垂直になってしないときは同じ大きさの力が同じところにはたらいても、力のモーメントは小さくなります。
下の図のような向きに、力がはたらいている場合、力Fを、スパナに垂直な分力と、平行な分力とに分解してみます。
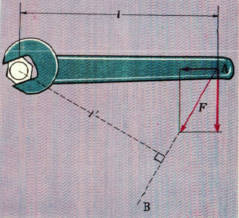
スパナに平行な分力は、スパナを回転させるはたらきをしていません。
スパナを回転させようとする力は、垂直な分力だけです。
この力は力Fより小さいので、力のモーメントも小さくなります。
力を分解して考えるかわりに、力のはたらいている方向(AB)に支点から垂線をおろし、その長さを力点と支点との距離(l’)にして考えてもよいのです。
この方法でもとめた力のモーメントは力を分解した場合と同じになります。