てこのはたらき
私たち人類は、過去のいろいろな経験をもとにして現在、すばらしい科学文明を築き上げました。
私たちはそのなかで生活していますが、長い人類の歴史から見るとこれは、ごく最近のできごとです。
人間が、道具らしい道具を使うようになったのはあの大きなピラミッドで知られている数千年前のエジプト時代のことです。
それまでの何万年、何十万年もの長いあいだはほとんど道具を知らないで、大自然の中で暮らしていたのです。
ですから、エジプト時代になって発明されたてこ・滑車・輪軸・斜面・ころなどの道具は人間にとって、実にすばらしい発明であったわけです。
しかも、現代のいろいろな機械もこれらのかんたんな道具がもとになっているのです。
これらの道具は小さい力で大きな力を出すこと力の向きを便利な方向にかえることなどのはたらきをしています。
中でも、てこは、そのもとになるもので人類の親友とも言われています。
てこのつりあいの実験
太さのいちような、長さ40センチあまりの棒をその中央部に穴を開けて、ひもでつるします。
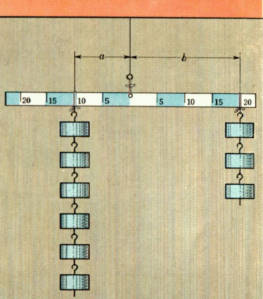
棒が水平にならないときには棒のかたはしを少し削って、水平になるようにします。
この棒には、中央から左右に、5センチおきに目もりをつけておきます。
また、棒のほかに、重さの同じ重りを、20個ほど用意します。
まず、棒の左側で中央から10センチはなれたところに重りを6個かけ、右側の20センチのところに別の重りをつるして棒が水平になるように、重りの数を加減します。
そして棒がちょうど水平につりあったとき右側の重りが何個になっているかを調べます。
つぎに、右側につるす重りの位置を15センチ・10センチ・5センチにかえて、それぞれの場合に重りが何個のとき、棒がちょうど水平になるかを調べます。
また、左側の重りの位置をかえたり、重りの数を多くするか少なくするかしておいて、まえと同じように実験を繰り返します。
これらの実験の結果をまとめてみると、上の表のようになりました。
この表から、つぎのような関係が成り立っていることがわかります。
「棒がつりあっているときには、棒の中央から重りまでの距離と重りの重さをかけた値は左側と右側とで、いつも等しくなっている」
これを式であらわしてみると、
a × P = b × Q
という関係になります。
a……棒の中央から左側の重りまでの距離
P……左側の重りの重さ
b……棒の中央から右側の重りまでの距離
Q……右側の重りの重さ
てこの三点
まえの実験のように、棒のつりあいを考えるときには棒を支えている点を、てこの支点と言います。
また、重りをつるしてある2つの点をともに、てこの力点と言います。
てこを道具として利用する場合には、てこに力を加えるところを力点、てこに力を出させるところを作用点と言って、区別しています。
てこの原理
まえの実験でわかったように、棒の2点に平行な2つの力、P、Qがはたらいてつりあっているときにはいつもつぎの関係が成り立っています。
この関係を、てこの原理と言います。
この式からわかるように、bがaの3倍であればQはPの3分の1の大きさでつりあいます。
ですから、支点の近くに作用点をとり支点からはなれたところに力点をとると小さい力で大きな力とつりあわせることができます。