三力のつりあい
1つの物体に、3つの力がはたらいていて物体が動かないでいることがあります。
このときには、3つの力の大ききと向きのあいだに特別な関係が成り立っています。
三力のつりあいの実験
机の上に大きな白い紙をしいてその上で、つぎのような実験をしてみましょう。
同じばねばかりを、3つ用意します。
その先にひもをつけて、3本のひものはしを結びあわせます。
つぎに、3つのばねばかりを、それぞれ勝手な方向に引っ張ってひもがピンと張り、ひもやひもの結び目が動かなくなったときに3つのばねばかりの目もりを読みます。
このとき、3本のひもの位置と結び目の位置を正確に紙の上にうつしとります。
白紙にうつしとった図について、つぎのような作図をします。
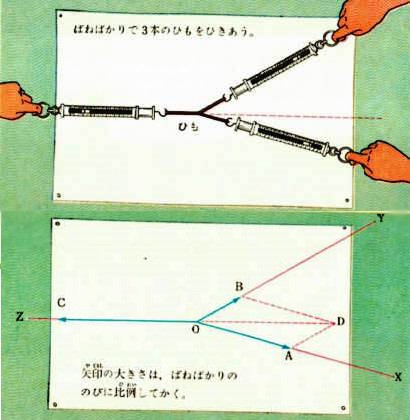
ひもの結び目をO、3本のひもの方向を、それぞれOX・OY・OZと書きます。
つぎに、先に読みとった、ばねばかりの目もりの読みの数に比例するような長さを、OX・OY・OZ上にOからはかって印をつけ、これらをOA・OB・OCとします。
すると、この3つの矢印、OA・OB・OCはそれぞればねばかりで引っ張った、3つの力をあらわしています。
つぎに、OAとOBを隣り合った二辺とする平行四辺形をつくります。
その対角線を引いて、これをODとします。
このODと、前に書いたOCとをくらべてみるとOCとODは一直線上にあって、長さが等しくなっています。
また、OBとOCを二辺とする平行四辺形をつくって対角線を引き、それとOAをくらべてみると、やはり長さが等しく一直線になっていることがわかります。
OCとOAについてやってみても同じような関係があります。
これらのことから、つりあっている3つの力のあいだには必ず次のような関係がなりたっていることがわかります。
「つりあっている3つの力のうち、2つの力でつくった平行四辺形の対角線は残りの1つの力と一直線になっていて、その向きは反対で大きさは等しい」
力の合成
まえの実験で、OCとODとは、一直線になっていて向きが反対で等しい大きさの力ですから、つりあうのは当然です。
しかし、実際にはたらいているのはODではなくて、OAとOBです。
ですから、OAとOBの2つの力のはたらきはODの力のはたらきと全く等しいことがわかります。
このように、2つの力のはたらきと全く等しいはたらきをもっている力を、合力と言います。
ODの力は、OAとOBの力の合力です。
また、合力をもとめることを力を合成すると言います。
平行四辺形の法則
同一の点にはたらいている2つの力、PとQを合成してその合力Rをもとめるには、まえの実験のようにPとQをあらわす矢印を二辺として平行四辺形をつくりその対角線Rを書けば、その欠印Rが合力になります。
このようなやり方を、平行四辺形の法則と言います。
2つの力PとQが、同じ直線上にないかぎり必ず平行四辺形をつくれますから合力をもとめることができます。
PとQが一直線になっているときは、平行四辺形をつくれないのでつぎのようにして、合力をもとめます。
PとQが同じ向きのときは、PとQの大きさの和に等しい長さの矢印を同じ直線上に、同じ向きに書くと、それが合力になります。
また、PとQが反対向きなら、PとQの大きさの差に等しい長さの矢印を、同じ直線上に、大きいほうの側に書くと、それが合力になります。
もし、PとQが等しい大きさならばその差はゼロになりますから、矢印は書けません。
このことを「合力はゼロである」とか「合力がゼロになる」と言います。
つりあっている二力の合力は、ゼロになっています。
3つの力、A、B、Cの合力は平行四辺形の法則を二度繰り返して使うともとめられます。
それには、まず、AとBの合力を平行四辺形の法則を使ってもとめてDとします。
続いて、DとCとの合力を同じようにしてもとめて、Rとします。
すると、Rが、A、B、Cの合力になります。
BとCを先に合成しても同じです。
前の実験のように、つりあっている三力のときは、合力がゼロになります。
力の分解
1つの力Rを、この力と同じはたらきをする二力、PとQとにおけることを力を分解すると言います。
そして、P、Qを、力Rの分力と言います。
力の分解は、力の合成と逆になっていますから平行四辺形の法則が成り立っているように、わければよいのです。
それには、つぎのようにします。
力Rをあらわす欠印が、対角線になっているような平行四辺形をつくると、その対角線をはさむ二辺が、分力PとQになります。
しかし、このような平行四辺形は、いく通りでも書けますから分力P、Qの組みは無数にもとめられます。
そこで、分力の1つの大きさと向きを決めておくか2つの分力の向きを、それぞれ決めておかなければなりません。
すると、決まった1組みの分力がわかります。
互いに直角になっている、2つの分力に分解するには図③のように、矢印Rの先から直線OX、OY上に垂線をおろしてそのあしをA、Bとします。
すると、欠印OAとOBが、もとめる分力、P、Qになります。
なぜならRは、PとQでつくる平行四辺形(この場合は長方形)の対角線になっているからです。