柱と梁
鋼や木材などで棒がつくられますが建築物や構造物で棒が縦におかれて圧縮応力を受けるように使われるとそれは柱と呼ばれます。
棒が、おもに横におかれて、曲げの応力やずれの応力(せん断応力)を受けるように使われるとはり、または、けたと呼ばれます。
これらの棒の断面の形には、円形や長方形をしたものやI形・L形・U形をしたものなどがあります。
梁にはたらく力
板ばねの実験で、下じきを使いましたがこれがもし細長ければ、はりと見なせます。
片方だけを固定したはりを、かたもちばりと言います。
また、両はしに支点をおいて支えたはりを、両端支持ばりと言います。
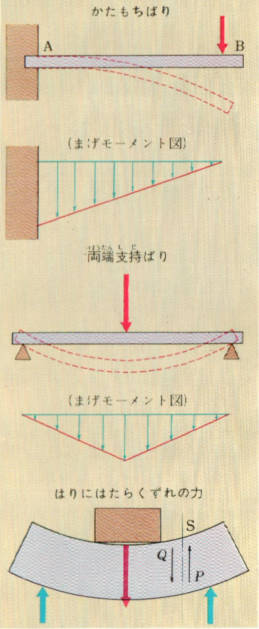
片持ち梁に、図のように重りをのせたときは固定したはしに近いほど、大きな曲げのはたらきを受けます。
両端を支えたはりで、中央に重りをのせたときは中央に近いほど、曲げのはたらきは大きくなります。
このように、材料を曲げようとする力のはたらきを曲げモーメントと言います。
それぞれのはりの下に書いた図形ははりの各点にはたらく、曲げモーメントの大きさをあらわしたものです。
はりには、このほかに、ずれの応力がはたらきます。
図で、はりのある断面Sを考えますとその右側はPのように動こうとし、片側はQのように動こうとします。
このため、Sの面の両側では、上下にこすり合うようなずれの変形を起こそうとします。
このように、はりには、各種の応力がはたらくので建物や橋などに使うには両方の変形について破壊に対する強さの大きいことが必要なわけです。
断面の形と材料の強さ
同じ材質のはりでも、断面の形によって、その強さが違います。
そこで、模型飛行機に使うヒノキの角棒やスギばしを使って、その実験をしてみましょう。
実験1
辺の長さが、5ミリと2ミリの長方形の断面をもつ角棒をせまい面を下にして、2つの台のあいだにわたします。
台の間隔は、30センチから80センチのあいだに選びます。
角棒の中央に、10円銅貨(約4.5グラム)を、1枚・2枚……とのせていきものさしで、中央部が何ミリ下がっていったかを測ります。
つぎに、広い面を下にして、まえと同じように中央部のたわみを測ってみます。
すると、せまい面を下にしたときよりも、たわみが大きくあらわれます。
この実験から、同じ材料を使っても、せまい面を下にしたときと広い面を下にしたときとで、曲がり方が違ってくることがわかります。
はりとして使う場合には、力が加わったときに曲がり方をできるだけ小さくするように工夫しなければなりません。
実験2
こんどは、材料の強さについて、実験してみましょう。
まえと同じヒノキの角棒を、長さ10センチに切ります。
自動上皿測りの皿に、うすいマッチ箱か、丈夫な洗濯ばさみを立ててこの角棒を折る支点とします。
まず、角棒の中央部を、せまい面を下にして支点にあて両はしをもって強く下に押し付けます。
そして、角棒が折れる寸前のはりの目もりを呼んでおきます。
つぎに、同じ角材を、まえと同じ長さに切り、広い面を下にして同じような実験をしてみます。
このときは、まえよりずっと小さい力で折れます。
木材は金属と違って、材質がいちようでないうえに破壊にむらが多いので、実験のたびに、かなり違った結果がでます。
そこで、この実験はなるべく数多くやって、その平均をとるようにします。
つぎの実験結果は、それぞれ10回やって、その平均をとったものです。
断面が5ミリと2ミリの長方形で、長さ10センチのヒノキの角棒ではせまい面を下にすると、だいたい2.2キログラム重の力で折れました。
広い面を下にしたときは、1.2キログラム重で折れました。
断面の形が、一辺が2ミリの正方形の角棒でやってみますと0.6キログラム重の力で折れました。
棒の強さ
このような実験から角棒は、同じ厚さなら、幅の広いほうが折れにくく同じ幅なら、上下に厚いようにおいて曲げたほうが折れにくいことがわかります。
家をつくるとき、はりや、床板を支える横木(ねだ)を上下に厚いように使うのは、このためです。
中央の支点のところで折れたのはここで、曲げモーメントがいちばん大きくなるからです。
木の枝は、つけねほど太く、先にいくほど細くなっています。
これをかたもちばりと考えると、つけねに近いほど枝の重みによる曲げモーメントが大きくなります。
したがって、木の枝は、それに伝えるのに都合のよい形をしていることがわかります。
木のぼりをしたとき、枝の先のほうにつかまると折れやすいのでなるべくつけねの近くに体重をかけます。
つけねにはたらく曲げモーメントの大きさはつけねからの距離に体積をかけたものになりますからつけねに近いほど、体重による曲げモーメントが小さくなるわけです。