組み合わせによる強さ
木平鋼の棒を組み合わせて、家や橋や塔などをつくりますがその組み合わせ方によって、強さが違ってきます。
形鋼の場合は、まえの組み合わせばりの例のように各部分の力のかかり方によって、いろいろな組み方ができるので便利です。
つぎに、棒を組み合わせた場合、その組み合わせ方によって強さがどのように違うか、調べてみましょう。
実験1
つぎの①図のように、マッチの軸木を四角形にならべ四すみを輪ゴムでしばります。
これとは別に、②図のように、軸木を三角形に組んでやはり輪ゴムでしばります。
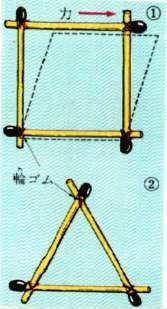
これを指で引っ張ったときどちらか形がかわりやすいかくらべてみましょう。
①のほうは、すぐ点線のようにひし形になりますが②のほうは、なかなか形をかえません。
このように、棒を三角形に組むと、たいへん丈夫になります。
そのため、三角形の組み方は、建物や橋などに、広く利用されています。
棒と棒をつないで組み立てた構造物を骨組と言い、そのつなぎめを、節点と言います。
また、骨組の棒が、つなぎめで自由に回転できるときはこのつなぎめを滑節と呼びます。
また、ピンでつながれているとも言います。
滑節では、棒と棒とのあいだの角度は、自由にかえられます。
木造や鉄骨の建物の骨組は、ふつう、滑節と見なされています。
トラス
すべてのつなぎめが滑節であるような骨組をトラス(沿節骨組)と言います。
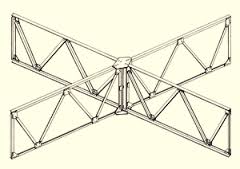
棒が、三角形の網目のように滑節でつながれている骨組は、代表的なトラスです。
トラス橋の両側の骨組は、これにあたります。
実験2
まえの実験でつくった、①図のような四角形の枠につぎの図のように、軸木ABをゴムひもで縛り付け四角形の枠を引っ張ってごらんなさい。
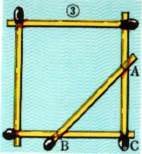
こんどは、四角形の枠が、丈夫になっています。
これは、ABCという、丈夫な三角形の枠ができたからです。
木造建築で、柱と柱のあいだに、すじかいという、ななめの棒を入れたり、はりと柱のあいだに、方づえという棒を入れたりするのはこれと同じ理由からです。
実験3
マッチの軸木を、輪ゴムで組んで、三角形ABCをつくります。
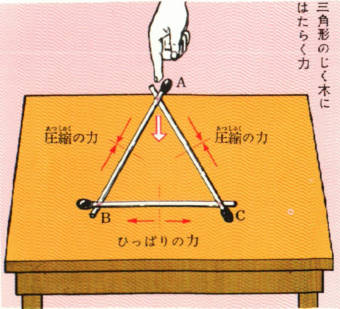
これを、下の図のように机の上に立て、Aのはしを上から押してみます。
このとき、つなぎめの動きを観察して、軸木の各部分に
どのような力がはたらくか、調べてみましょう。
A点の輪ゴムは、下のほうに動いて
AB・ACの軸木を、下にめりこませようとします。
これは、AB・ACに、圧縮の力がはたらいていることをしめします。
B点の輪ゴムは左へ、C点の輪ゴムは右へ、ずるずると滑ろうとします。
このことから、BCの軸木には、引っ張りの力がはたらいていることがわかります。
ですから、BCの棒を丈夫な糸や針金とかえても
このような外力にたえることができます。
棒をピンでつないだ、トラスでは、それぞれの棒は
おもに引っ張りの力、または圧縮の力のみを受けます。
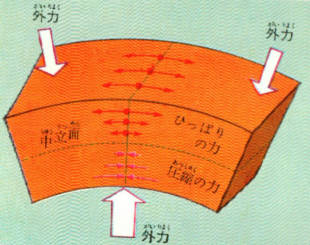
棒の組み合わせに、外力をかけた場合に、外力の加わり方によって
それぞれの棒に生じる応力の性質や、大きさが違ってきます。
そのため、それぞれの棒は断面の形や太さなどを、適当に選ばなければなりません。
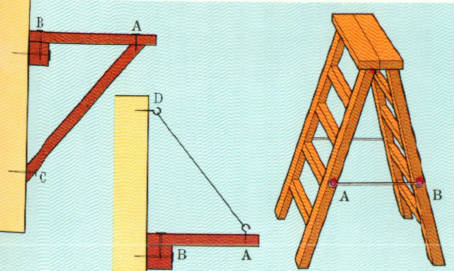
脚立は、両あしを開いて立て、その上にのぼって、仕事をするのに使います。
この場合、図のように、太い針金ABをかけると
両あしが開かないのは、ABが、張力に耐えているからです。
たな板ABをつるとき、Bのところを釘づけするだけでは弱いので
ACのような支え棒を入れると、重い物をのせることができます。
この場合、ACは圧縮の力に耐えるだけの、太い棒を用います。
また、ADのように針金でつることもできます。
ラーメン
トラスとは反対に、棒と棒とのつなぎめが、すべて硬くつないである骨組もあります。
これは、骨組が変形しても、つなぎめのところで棒と棒との用度が、全くかわりません。
このようなつなぎめを、剛節と言い。
剛節でつながれている骨組を、ラーメン(剛節骨組)と言います。
鉄筋コンクリートや、鉄骨鉄筋コンクリートの柱とはりのつなぎめは剛節と見なされます。
下の①図のようなトラスに、左から押す力が加わると点線のような形になり、はりABにも、柱AD・BCにも、曲げの力が加わりません。
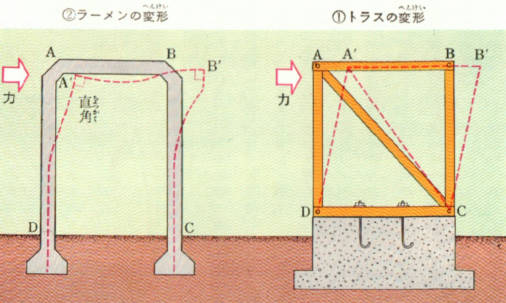
②図のラーメンでは、左から力を加えるとつなぎめのAやBのところの角度がまったくかわらないので点線のように変形します。
この場合は、柱がA’D、B’Cのように曲がるだけでなくはりABも、点線A’B’のように曲がります。
ラーメンでは、骨組の一部に加わった曲げの力が、ほかの部分にもわけられるため、骨組の一部にだけ、大きな力が集まることがありません。
このためラーメンもトラスとともに橋やそのほかの構造物の骨組として、使われています。