重心
手に持っているものをはなすと、そのものは必ず地面に落ちます。
このように、地球上にあるすべての物は地球から力を受けて地球の中心の方向にひかれています。
この力を、私たちは重力と呼んでいます。
この重力の大きさがその物の重さと呼ばれているものです。
また、物の重さは、グラムという単位で測ることができます。
たとえば、重さが100グラムの物といえば、重力が100グラムの大きさでその物をひいていることになります。
その重力は、図のように、物を細かく同じ大きさにわけて考えてみるとどの部分にも、同じ大きさではたらいています。
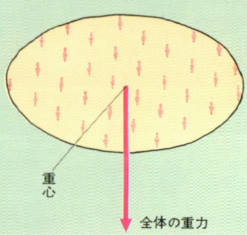
そして、どの力も地球の中心の方向に向かっています。
これらの力を全部加え合わせた大きさが、100グラムの力なのです。
ところが、このようにたくさんの平行な力はいつでも全部1つの点に集めて考えることができます。
つまり、1つの点に100グラムの力がはたらいているのと、同じことなのです。
この力のはたらく点を、私たちは、その物の重心と呼んでいます。
このことは、つぎの実験からも確かめることができます。
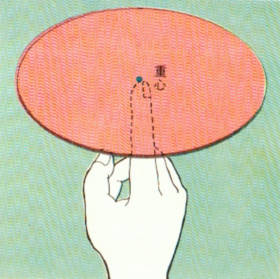
まず、図のような円板について考えてみましょう。
この場合、円板のどの部分にも、重力がはたらいていることは、まえと同じです。
しかも、それらの重力は全部1つの点に集まってはたらいていると考えることができるならば、この円板をその1つの点て支えることができるはずです。
そして、そのときの力は、その円板の重さと同じはずです。
そこで円板を中心近くのいろいろな点で支えてみましょう。
何回か試しているうちに確かに円板は、1つの点で支えられることが確かめられます。
したがって、その点が円板の重心でだいたい円板の中心に一致していることがわかります。
円板の場合には、その中心が、およその重心であることは見当もつきますが不規則な形の板である場合には何回か試してみて支えられる点を探しださなければなりません。
重心のもとめ方
重心をもとめるには支えられる1つの点を探すやり方のほかにつぎのような方法があります。
鉛直線の交点からもとめる方法
重心の位置がわかっている図のようなうすい板を図のA点につけた糸でつりさげると、いつでもA点の真下に重心がきます。
つまり、板の重心は、A点からおろした鉛直線の上にあることがわかります。
この結果を利用すると、いろいろな板の重心をもとめることができます。
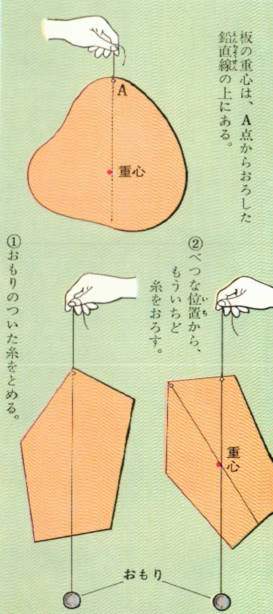
たとえば、図のような形の板の重心をもとめてみましょう。
まず、板のふちに1つの点をとります。その点に、重りのついた1本の糸の途中をとめます。
そして、糸のはしをもって、これらをつるすと図のように、糸は1本の鉛直線になります。
したがって、板の重心は、この線の上のどこかにあるはずです。
そこで、糸にそって、板の上にえんぴつで1つの点を印その点と糸をとめた点とをむすぶ線をひいておきます。
つぎに、別な位置に、もう1つの点を選び、まえと同じ実験を繰り返して鉛直線を板に書きこめば、この直線も、また重心の上を通っているはずです。
したがって、この板の重心は、2つの直線の交点であることがわかります。
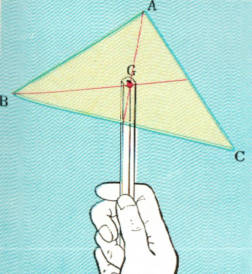
また、三角形の板の重心は、図のような作図によっても、もとめることができます。
この場合、三角形の重心は頂点Aと底辺BCの中心をむすぶ直線の上の、どこかにあるはずです。
また、頂点Bと底辺CAの中心をむすぶ直線の上にもあるはずですからこれらの中線が交わる点Gが、この三角形の板の重心になります。
棒状の物の重心をもとめる方法
長い棒のような物の重心をかんたんにもとめるにはえんぴつを2本用意して、その棒を、2本のえんぴつで水平に支えます。
そして、静かに2本のえんぴつを水平のまま、互いに近づけます。
えんぴつが次第に近づいて最後に2つがくっついてしまっても棒は水平のまま上にのっています。
したがって、その棒の重心はくっついた2本のえんぴつの中間にあることがわかります。


