単振動
ふりこの振動のような運動を単振動と言います。
下の図のように、つるまきばねに重りをつるし、Bまで引き伸ばしてはなすとOを中心としてAとBのあいだで振動します。
これも、単振動です。
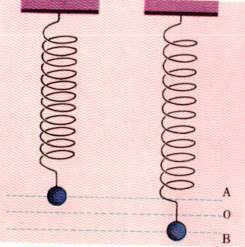
このときは、重力と、つるまきばねの弾力とがはたらくので弾性振動とも言います。
腕時計のひげぜんまいは、図と形は違いますが、同じ単振動をします。
いろいろの楽器や、マイクロホン・スピー力ーなどの振動はすべて弾性振動ですが、ふりこや、つるまきばねにつるした重りの振動のようにかんたんな振動ではありません。
固有振動
鉄をU字形にし、そのあしに、木箱(共鳴箱)を取り付けたものを音叉と言います。
音叉を、木づもで軽く叩くと、きれいに澄んだ音がでます。
これは、音叉が振動をして、この振動が空気に伝えられ、音波になるからです。
音叉が振動していることは、その先を、少し水面にさしこんでみれば、わかります。
音叉の振動や、これを伝える空気の振動などで1秒間に振動する数を、その振動数と言います。
振動数に、その振動の周期をかけると1になるという関係かわりますから1を周期で割ると振動数がもとめられ、1を振動数で割ると周期をもとめることができます。
音叉は、その形や大きさ、材料にした鉄の性質などによって決まる一定の振動数をもっています。
これを、固有振動数と言います。
音叉だけでなく、すべての物体は、叩けば必ず音がでます。
その振動数は、その物体の形や弾性によって決まる、一定の大きさをもっています。
このように、物体が、固有振動数で振動することを、固有振動と言います。
自由振動と強制振動
ふりこや音叉の振動のように、はじめに外から加えられた力だけで物体が振動することを、自由振動と言います。
自由振動では、固有振動の振動数で振動し振動を続ける力がはたらかなければ、しだいに振動が止まってしまいます。
このような振動を減衰振動と言います。
ぶらんこに子どもをのせて、いちばん下にくるたびに少しずつ押してやると、しだいに大きく揺れていきます。
このように、ある物体が自由振動をしているとき、一定の周期をもった力をたえず外から加えると、振幅が大きくなります。
この力を強制力と言い、強制力によって起こる振動を、強制振動と言います。
ぶらんこが、いちばん下にくるたびに動く方向と反対向きの力を少しずつ加えると振幅がしだいに小さくなって、ついには止まってしまいます。
このように、強制力は振動を強めることも、弱めることもできます。
振動の共振
すべての物体は、それぞれ固有振動数をもっています。
この固有振動数に等しい強制力を加えると、その物体は、しだいに振動しはじめます。
このことを、共振または共鳴と言います。
図のように固有振動数の等しい音叉AとBを向い合せておき一方を叩いて振動させます。
しばらくして、叩いたほうの音叉を手で握り、その振動を止めて耳を傾けると叩かなかった音叉が、鳴り出しています。
そのわけは、つぎのように説明できます。
まず、Aの振動が空気に伝わり、音波ができます。
音波は、進行方向に圧力をもっていますからその圧力が強制力となって、Bをごくわずかずつ押し動かします。
この場合、Bの固有振動数は、強制力の振動数と等しいのでBの振動が音波のくるたびにさかんになって、鳴り出すのです。
また、つぎのような実験をしてみましょう。
下の写真のように、1本の糸を水平にはり、長さの同じふりこAとBをむすびつけます。
はじめ、AのふりこをふらせるとAの振動が弱まるにつれて、Bが大きくふれてきます。
Aの振動が止まると、Bの振動がもっとも大きくなりBの振動が弱まると、しだいにAの振動が強くなります。
そして、これが繰り替えされます。
これも、振動の共振です。
2つのふりこの長さが等しいので、固有振動数も等しくなります。
このため、一方のふりこの振動が水平にはった糸を伝わってもう1つのふりこを動かすのです。
電車が振動するときは、そのときの車体の振動数に等しい固有振動数をもつつりかわが共振して大きく揺れ動きます。
つり橋をわたるとき、足なみが橋の固有振動数とあうと橋は大きく揺れだします。
これも、共振の例です。
したがって、つり橋をわたるときは数人で足なみをみだしながら歩くほうが安全です。