カテゴリー: 力の利用

ばねの利用

弾性をもつ物は、ばねとして広く利用されていますがひとくちにばねと言っても、その目的によってそれぞれ違った使い方をしています。

ばねに仕事をさせる

ばねに力を加えて変形させると外力はその力に動いた距離をかけた値と同じだけの仕事をします。

これは、変形のエネルギーとしてばねに蓄えられ、ばねがもとにもどるときに同じ量の仕事をします。

この性質を利用したものに、時計のぜんまいがあります。
ぜんまいをまいておくと、変形のエネルギーを、少しずつ仕事にかえて時計の歯車や針を、摩擦力に逆らって動かしていきます。

また、洋服ブラシは、毛の弾性を利用して小さいごみを跳ね飛ばすものです。

物をおさえる

洗濯ばさみや紙ばさみなどはつるまきばねの弾性を利用して物をおさえるものです。

電気のスイッチにも、銅板の弾性が利用してあります。

自転車のスタンドにも、つるまきばねがついていてスタンドをあげたとき、水平に保つはたらきをしています。

ボイラの安全弁をおさえておくためにも、ばねが使われます。
これは、ボイラの蒸気が、一定の圧力以上になったとき弁を押し開いて安全を保つようにしたものです。

衝撃や振動を弱める

自動車や鉄道車両は、運転中に、いろいろな衝撃の力や、振動を受けます。
そこで、車軸と車体のあいだに、重ね板ばねやつるまきばねを使ってこれらの力を弱めています。

椅子やベッド、自転車のサドル、オートバイなどについているつるまきばねも同じようなはたらきをしています。

列車の連結器には、輪ばねをならべて使ったものがあります。
これは、内輪ばねと外輪ばねを組み合わせたもので互いに円錐形の面で接しています。

輪ばねに、軸の方向から力が加わると内輪ばねは圧縮され外輪ばねは押し広げられます。

このため、触れ合っている面に大きな摩擦力もはたらき、衝撃の力を弱めることができます。

力の大きさを測る

ばねは、弾性限度内では、フックの法則によって外力と変形の量が比例します。

この性質を利用すると、変形の量をはかって加えた力の大きさを測ることができます。

ばね測りや上皿測りは、つるまきばねを使ったものです。電流計の針の軸に、うずまきばねをつけたものもあります。

これは、ばねの変形によって、電磁気力を測るものです。

また、ねじり測りといって、針金のねじれによって力のモーメント、または、重さを測るものもあります。

ゴムとその利用

ゴムは、金属にくらべて、著しく弾性による変形をします。
もとの長さの数倍に伸ばして千切れないし、力を取り去るとまたもとの長さにもどります。

ゴム測りの実験

輪ゴムを8本ばかりつなぐか、ゴム糸を50センチあまりとってそのはしに、小さい皿をつるします。

皿は、フィルムの空き缶のふちに、小さい穴を3つ開け細い針金を通したものでよいでしょう。

ゴム糸の上のはしを高いところにとめて、下につるした皿に重さのそろった鉄の玉かガラス玉を、1個ずつのせていきます。

玉をのせるたびに、玉の数とゴムの長さを測って、その関係をグラフに書いてみましょう。

鉄の玉の重さが、1個1.5グラムのときその結果は、つぎのグラフのＡＢＣのような曲線になりました。

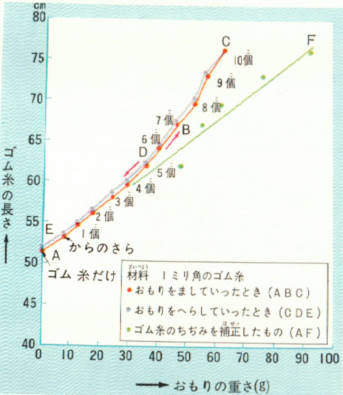
この場合、皿の重さ7.5グラムの中に、4個の鉄の玉を加えたところまでは、びと重りの数とが比例するとみて、差支えありません。

それ以上になると、伸びの増える割合いが大きくなり上のほうに曲がった曲線になります。
それでも、せまい範囲を見れば直線に近く、比例していると見なせます。

ゴム糸を注意してみると、伸びが増すにしたがって、細くなります。

したがって、ゴム糸の断面にはたらく応力をくらべてみると細くなったときのほうが、実際には、大きくなっているはずです。

そこで、ゴム糸の太さを測って、まえのグラフを補正するとほぼＡＦのようになりました。

こんどは、鉄の玉を10個のせたＣ点のところで1個ずつ玉を減らしていくと、ＣＤＥの曲線を描いてもとにもどってきました。

この場合は、ＡＢＣの曲線と少し食い違っていて伸びが残っていることがわかります。

ゴムの利用

ゴムは、変形したときに生ずる力で、物を締め付けるのによく使われます。
ゴムひもはバンドに使ったり、包み紙をとめたりするのに使われます。

模型飛行機のプロペラをまわすにはゴム糸をねじったときそれがもどろうとするときの力を利用します。

ゴム管は、それをはめたものとよく密着します。
そのうえ、気体や液体を通しにくく、曲がりやすいので水辺やガスのホースに使われています。

入れ物のふたに、ゴムのパッキンを使うのもゴムの弾性で隙間をなくすためです。

このほか、衝撃や振動を弱めるためにも、ゴムが使われます。

自転車や自動車のタイヤなどが、そのよい例ですがこの場合は空気の弾性が助けになっています。

ばねの伸び縮み

ロバート＝フック（1635～1703年）というイギリスの物理学者はつるまきばねに重りをつるす実験をして有名なフックの法則を発見しました。

これは、つるまきばねにつるした重りの重さとつるまきばねの伸びの長さが、比例するという法則です。

つるまきばねの、下のはしに重りをさげるとばねが伸びて、下のはしがさがります。

そこで、このばねの下のはしの位置の読みを縦軸にとり重りの重さを横軸にとって、その関係をグラフにあらわすと下の図のＡＢの直線が書けます。

この図で、伸びはＡ点での位置との差です。

もし、つるまきばねの下のはしに上向きの力（圧縮の力）を加えてばねが縮むなら、この力に対して、ばねの縮みが比例します。

この場合の関係も、図のＡＣの直線であらわされます。

しかし、つるまきばねでも無制限に力を増すと変形と力が比例しなくなります。材料と寸法によって、それぞれ決まった限界があります。

つぎに、つるまきばねに重りをつるしたときの力のつり合いを考えてみましょう。

上の図で、重りＰの重さは、重りにはたらく重力の大きさＷです。
重りは静止しているので、この重力を打ち消す力fが反対方向にはたらいていなければなりません。

この力fは、ばねが伸びたためにその内部に生じた弾性の応力によるものです。
したがって、ばねがfという力で、重りを上に引いていることになります。

もし、fより重りの重さＷが大きいとするとばねはさらに下に伸びて、だんだん弾性の応力fが大きくなります。
そして、ｆと重力Ｗが等しくなったとき、ちょうどつり合います。

実験では重りの重さＷと、ばねの伸びとの関係を調べましたがこれは、ばねの弾性の応力ｆと、ばねの伸びとの関係を調べたことと同じです。

このような実験で書いたグラフと、そのばねを使うと、重力にかぎらずほかの種類の力でも、ばねばかりの伸びによって測ることができます。

変形の種類とフックの法則

フックの法則は、つるまきばねの伸び縮みにだけあてはまるのではありません。

棒や板の伸び縮み・ねじれ・曲がりうずまきばねの軸のまわりの回転などの変形にもその材料の弾性限度内であれば、成り立ちます。

また、ずれの変形についても外から加えた力と変形の角度とのあいだに弾性限度内で、フックの法則が成り立ちます。

比例限度

弾性限度の近くでは、応力とひずみが、やや比例関係から外れてきます。
そこで、フックの法則が成り立つ限界の応力を、比例限度と言っています。

しかし、弾性限度と比例限度は、ほとんど一致すると見て差支えありません。

弾性と塑性

金属・石・木などは、ふつうの温度では形があまりかわりません。
このような物体を、円体と言います。

固体は、空気や水のような気体や液体にくらべると非常に変形しにくいものですが、ばねのところで調べたように固体でも変形させることができます。

変形の種類

円体に力を加えると力の加え方によって、変形のしかたが違ってきます。

固体の中でも、ゴムは変形が著しいのでゴム糸や消しゴム・スポンジなどを引っ張ったり、押したり、ねじったりしてその変形の様子を調べてみましょう。

力の加え方と、変形の様子をまとめてみるとつぎのような種類にわけることができます。

①伸び

両はしを引っ張ると、その方向に伸びる。

②縮み

両はしから押しつけると、その方向に縮む。

③曲がり

板ばねの実験のように、両はしを支えて、中火に力を加えると曲がる。
片はしだけ固定して、別のはしに力を加えてもよい。

曲がりは、一部分が伸びて、他の部分が縮んだ変形とみなされる。

④ずれ

上下の面で、面に沿って、反対方向に力を加えたときの変形。
見た目には、マッチの外箱を押し潰したような形になる。

⑤ねじれ

両はしをねじるときの変形。
まえに実験したように、つるまきばねの各部分は、これと同じ変形をしめす。

これは、ずれに基づいている。

⑥体積の変化

水の中に沈めたときのように、すべての方向からいちような力を加えると体積が小さくなる。

弾性と弾性変形

このように、力の加え方によって、固体はいろいろの形にかわりますが引っ張った場合について、くわしく調べてみましょう。

図のように上のはしを固定した棒を引っ張ると、その方向に伸びます。
このとき、力が大きいほど、伸びの量も大きくなります。
実験によると、引っ張る力Ｆと、伸びの量Ｘは比例します。

いま、この棒のもとの長さをl（センチ）とすると(x÷l）を伸びの割合と言います。

これは1センチあたりの棒の伸びをあらわします。
いっぱんに、変形の割合をひずみとも言います。

加えた力に応じて、棒の内部にも力がはたらいています。

いま、棒の断面積をＳ（平方センチ）とすると、（ｆ÷Ｓ）が棒の断面1平方センチふたりにはたらく力になります。

このようにあらわした、物体内部の力を応力と言います。
引っ張りの場合は、引っ張り応力と言います。

応力（f÷S）をひずみ（ｘ÷Ｓ）でわったものを、弾性率と言います。
引っ張りの場合は、伸びの弾性率ともヤング率とも言います。

弾性率は、それぞれの材料について形の大小に関わらず、一定の値を持っています。

棒に加えた力を減らしていくと、変形は次第にもどり全く力を取り去ると、もとの形にもどります。

このように、力を加えると形を加え、力を取り去るともとにもどる性質を、弾性と言い、このような変形を弾性変形と言います。

弾性限度

加える力が、ある大きさを超えると力を取り去っても変形が残るようになります。
このときの境目の応力を、弾性限度と言います。

塑性と塑性変形

物体に、弾性限度を超えた力を加えると力を取り去っても完全にはもとの形にもどらず変形が大分残るようになります。

このような応力の範囲では、物体は塑性をしめすと言います。
そして、この場合の変形を、塑性変形と言います。

したがって、塑性というのは、物体に力を加えて変形させたときその変形をそのまま残す性質ということができます。

銅線や鉛の板、ヒューズの針金などを曲げてみると曲がったままになりま
す。これは、塑性よる変形です。

塑性のことを、プラスチシティとも言います。
プラスチックというのも、これからきた言葉で、熱や圧力を加えた場合に、著しいそ性をしめす高分子物質を、ひっくるめて言います。

金属は、プラスチックとは言いません。

ベークライトは、熱によって変化し、しまいに硬くなります。
いったん硬くなると、もとにもどりません。

塩化ビニル樹脂は、熱すると、やわらかくなって変形しやすくなり冷えると、そのままの形を保ちます。鉄も、熱すると塑性を増すので。

自由に加工することができます。

私たちが使っている、機械や器具の大部分に塑性か利用してつくったものです。

実験

縫い針を1本用意して、指で少し曲げてみます。指をはなすとすぐもどります。
これは、針が鋼でできていて、弾性をもっているからです。

つぎに、この針を、マッチまたはガスの火で赤く焼いた後、板の上において自然に冷まします。

こんどは、これを指で曲げると、よく曲がります。
これは、塑性が著しくなったからです。

このように、鋼は焼きなますことによって、やわらかくなることがわかります。

つぎに、この針をもういちど赤く焼いた後、冷たい水に、急に投げ入れてみます。
これを取り出して、指で曲げてみると、こんどは硬くなっています。

このようにすることを、焼き入れと言います。
焼き入れによって、針には、ふたたび弾性が出てきましたがそのかわり、少しもろくなっています。

鋼の変形

鋼は、弾性の著しい金属ですが弾性限度以上の力を加えると、やはり塑性をしめします。

鋼を引っ張るとき、外力を一定にしておいてもずるずると伸び出す点があります。

この点の応力を、降伏点と言います。

降伏点を越えて、さらに引っ張っていくとしまいにはＦ点で切れてしまいます。

図は、これらの様子をあらわした、応力ひずみ曲線です。

この曲線で、Ｅ点の応力が、見かけ上もっとも大きくなっています。
このときの応力を極限強さと言い、実用上これで材料の破壊に対する強さをあらわします。

加工硬化

図のＧ点で、力を静かに取り去っていくと応力とひずみとの関係は、ＧＭのような直線になります。

この鋼にふたたび力を加えていくと、ほぼＭＧ線上の弾性変形をおこない、弾性限度は、まえより大きくなります。

そして、このときの弾性限度を越えると、ほぼ曲線ＧＦをたどります。
上の図で、たとえば、亜鉛に500パーセントのずれをあたえるとさらに変形を続けるには、はじめの約7倍の応力が必要です。

このように塑性変形で硬くなることを、加工硬化と言います。

ばねのいろいろ

ソファーを手で押したり、ソファーにこしかけたりするとソファーがもとにもどろうとしているのが感じられます。

これは、ソファーの中に、ばねがいくつもならべてとりつけてありそのばねが、押し返しているからです。

ばねは、その形によって、いろいろの種類にわけられますが板ばね、うずまきばね、つるまきばねが、おもなものです。

板ばね

板ばねは、板の形をしたばねで、鋼でつくってあるのがふつうです。

実験1

①図のように、セルロイドの下じきを
机のはしに半分だけつきだしておき、一方のはしを厚い本でおさえます。

下じきのつきでた部分に小石を1つのせ、つぎに、もう1つのせてみます。
すると、下じきのはしは小石をのせるにつれて、ますます下がります。

こんどは小石を1つずつ取り去ると下じきは、もとの位置までもどります。

この実験でわかるように、板ばねは外から力を加えると曲げることができ、その力が大きいほど、曲がり方も大きくなります。

また、外から加えた力を減らしていくと板ばねの曲がり方が減っていき力がすっかりなくなると、ふたたびもとの形にもどります。

下じきを曲げると、下じきの各点は少しずつ下がりましたが曲げによるこの変形の量を、その点でのたわみと言います。

こんどは、②図のように下じきを両はしで支えて真ん中に力を加えてみます。
このときの曲がりとたわみも、加えもとにもどります。

①と②のいずれの場合も、重りの重さとばねの1点のたわみとは、比例することがわかります。

実験2

こんどは、やや集めの下じきに本を載せて机の上におき、下じきのはしを少しだけ机のはしからだしておきます。

まず、げんこつで机を軽く叩いてみます。
つぎに、下じきのはしを、同じくらいの力で叩いてみます。

すると下じきは、叩くと同時に曲がってげんこつは痛みがずっと少なくてすみます。

木の板に釘を打ち込むときには板をしっかりした台の上に載せておくと釘がうまく入ります。

しかし、台からはみ出した板のはしに釘を打ち込むときには、板がはずんで、なかなか釘が入りません。
ことに、板がうすい場合には、なかなか打ちこめません。

この実験でわかるように板ばねはたわむことによって、衝撃の力を弱めるはたらきをします。

重ね板ばね

自動車や電車などには、車輪と車体とのあいだの衝撃を弱めるためにばねが取り付けてあります。
この場合には板ばねを数枚重ねた、重ね板ばねが多く使われています。

板ばねの両はしを支えて、真ん中に力を加えて曲げる場合には曲げようとするはたらきは、板ばねの両はしのところがいちばん小さくゼロになります。

ところが、中央に近いほど、曲げようとするはたらきが大きくなります。

そこで、中央に近いほど、板ばねの幅を広くすれば曲げによって内部に生ずる力が、どの部分もいちようになります。

しかしこの形では、ばねとして使うのに不便なので実際には図のように細長く切って中央の部分が厚くなるように重ねて使います。

これが重ね板ばねで、ひし形のばねと同じはたらきをします。

うずまきばね

うずまきばねは、蚊取り線香のように金属をうずまき形にまいたものです。
これには、断面の形が長方形でテープのようにまいた鋼が多く使われます。
時計に使われているぜんまいも、うずまきばねです。

実験

長さ20センチ、幅1センチのうすいブリキ、または、真鍮の板をえんぴつにまきつけて、うずまき形に曲げます。

図のように、Ａのはしを、マッチの軸木ＣＤに硬くまきつけて止めます。
Ｂのはしは、机のはしに固定します。

つぎに、マッチの軸木2本をＣＥ、ＤＥのように、糸で組みます。
Ｅのはしには、ＥＧのように、もう1本の軸木を硬く結びつけます。

さらに、針金で、同じ大きさのＳ字形のかぎを数個つくりその1つは、Ｅの部分につないでおきます。

このような装置ができたら、ＥのはしのかぎにＳ字形のかぎをつぎつぎにかけていき、だんだん長くしてみます。

かぎの数が増すにつれて、うずまきばねのＡのはしに固定してある三角形の軸木は、ＣＤを回転軸としてまわっていきます。

この場合、ばねを回転しようとするはたらき（力のモーメント）はかぎの列と軸木ＣＤとの最短距離（l）にＳ字形のかぎの数（n）をかけあわせた値、（l×n）に比例しています。

また、かぎの数を増していくと、ＥＧはＣＤを軸としてどれほどの角度だけ回転するでしょうか。
Ｇのそばに目もり板をおいて、その角度を調べてみましょう。

まわった角度と、まえの（l×n)は比例しているはずですがlがあまりかわらないので、まわった角度とnも、ほぼ比例するでしょう。

こんどはＳ字形のかぎを、だんだんに減らしていくとしまいには、もとの位置までもどって止まります。

うずまきばねの性質

うずまきばねの一方を固定し、もう一方のはしに力を加えてその中心の軸のまわりにまわしたときは、ばねの各部分は曲がっています。

このときの曲がり方は、まえの実験からわかるようにうずまきばねをまわそうとするはたらきが大きいほど、大きくなります。

また、力を取り去ると、もとにもどります。
このことは、板ばねの場合と同じです。

時計やおもちゃを動かすのに使われているぜんまいは中心の軸のまわりにまきこんだときそれがもとにもどろうとするときの回転力を利用するものです。

この場合の回転力は、ぜんまいの厚さや、幅が大きいほど大きくなります。

つるまきばね

針金、またはテープのような板金をアサガオのつるが竹にまきつくときのように、コイル形にまいたものをつるまきばねと言います。

このばねは、軸の方向に、伸びたり縮んだりすることができます。
そのときの変形は、針金や板金の各部が少しずつねじれることによって起こります。

つるまきばねも、衝撃の力を弱めるはたらきをするので交通機関をはじめ、ソファー・寝台など日常生活の道具にも広く利用されてします。

また、物をおさえつけるのに、つるまきばねの弾力を利用しているものもあります。

実験

画用紙を、長さ30センチ、幅1センチに切り、太い丸棒にまきつけて、つるまきばねの形にします。
この紙の両はしを、両手で左右に引っ張ってみると、紙はねじれています。

このことから、つるまきばねの伸び縮みは各部分のねじれによることがわかります。

リンク装置

4本の棒を、①図のようにつなぎあわせ、それぞれの棒がつなぎあわせた点のまわりを、自由にまわれるようにしておきます。

このようなしくみを、リンク装置と言います。

このリンク装置で、ａの棒を動かさないでおいてｂの棒をＯのまわりにまわすと、Ｃの棒はＱのまわりをまわれないでその先のＲの点が、ＭとＮのあいだを行ったり来たりします。

反対に、Ｃの棒をＭとＮのあいだで往復させるとｂの棒は、Ｏのまわりをぐるぐるまわります。

リンク装置は、このように回転運動を往復運動にかえたり往復運動を回転運動にかえたりするはたらきをします。

このようなリンク装置を実際に使うには②図のようにＯとＱの点にｂ・cの軸をつけて回転運動や往復運動をさせます。

また、①図で、ｄの棒の途中の点、たとえばＳの点の運動を調べるとＰの点が円運動をするとき、Ｓは楕円形の運動をします。

ｄの棒のかわりに、曲がった棒や板をつけてその上の1点を選んで運動させると8の字の形やいろいろ複雑な運動をさせることができます。

---

---

クランク仕掛け

まえのリンク装置の図で、Ｏを通る棒の回転軸とｂの棒をいっしょにすると、つぎの③図のように一部分が曲がった回転軸になります。

このようなものを、曲軸、またはクランクと言います。

このクランクに、ｄの棒をつなぐ点Ｐの回転軸をクランクピンと言い、ｄの棒のことを、連接棒と言います。

いま、クランクを図のようにまわすとリンク装置のときと同じように連接棒のはしのＲの点とぼうｃは矢印のような首振りの往復運動をします。

これと反対に、Ｒに首振りの往復運動をさせてクランクに回転運動をさせることもできます。

④図は、連接棒の先のＲをａの棒につけｄの棒を、ａの棒にそってだけ滑らせるようにしたものです。
この場合は、クランクを回転させるとＲが棒ａの直線上を往復運動します。

このように、クランク、またはその原理を使って回転運動を往復運動にかえたり往復運動を回転運動にかえたりするしくみをクランク仕掛けと言います。

クランク仕掛けで、ａの棒の両はしの位置、ＯとＱが決まっていて動かなければ、ａの棒はなくてもよいわけです。
そのため、実際のクランク仕掛けには、ａの棒はあまり見られません。

クランク仕掛けの利用

クランク仕掛けは、蒸気機関や自動車のエンジンなどで大切なはたらきをしています。

また、私たちの生活に使われている機械にも、いろいろと利用されています。

下の図の①は、ミシンのはずみ車をまわすベルト車と足踏み板とのあいだのクランク仕掛けです。

②図は、足踏み脱穀機に使われている足踏み板と車とのあいだのクランク仕掛けです。
これらは、足踏み板の往復運動を、回転運動にかえるためのものです。

③図は、こうもりがさの骨のはたらきをしめしたものです。
Ｏとｂはクランクではありませんがクランクと同じはたらきをしています。

Ｒが、かさのえを上下に滑ると、クランクピンにあたるＰの点がＯのまわりに円を描いて、かさを広げたり、つぼめたりします。

上の図の右は、自動車のエンジンに使われているクランク仕掛けです。
連接棒の先についているピストンは、ガスの爆発で押されてクランクを回転させます。

上の図の左は、飛行機に使われている、7シリンダの星型エンジンです。
これは、それぞれの連接棒が、共通のクランクピンにつながれています。

クランクの死点

蒸気機関車のクランク仕掛けで一定の力でピストンを押しているとすると、連接棒にはたらく力も一定です。
しかし、クランクをまわす力はクランクピンのまわる位置によって違います。

下の図のように、連接棒がクランクの回転軸を通るときと連接棒を延長した先が、クランクの回転軸を通るときクランクの回転力はゼロになります。

クランクピンが、このような位置にきたときをクランクの死点と言います。

クランクが死点にあるときはいくら連接棒に力を加えても、クランクはまわりません。

そこで、蒸気機関車の両側の動輪はクランクピンの位置を90度だけずらして、一方が死点にあっても他方が死点にならないようにしてあります。

また、動輪の一部が、とくに重くつくられているのはその慣性によって死点で止まらないようにするとともに回転を滑らかにするためです。

自動車のエンジンでも、ピストンが1つだけではちょうど死点の位置にくると、クランクがまわりません。

このために、ピストンをいくつもつけてしかも、クランク軸へ取り付ける角度をかえて滑らかな回転ができるようにしてあります。

また、クランク軸についているはずみ車も、死点で止まるのをふせぎ回転を滑らかにするはたらきをしています。

カム

軸といっしょにまわる物の外側のふちに棒を、いつも触れ合うようにしておきます。

このとき、軸といっしょにまわる物が不規則な形をしているとこれに触れている棒は、そのふちのでこぼこに応じて出たり入ったり、直線運動をします。

このようなしかけを、カムと言います。

図のようなカムでは、棒が円形の部分に触れているときは動きません。
回転する板がつきでているところに、棒が触れるときだけ上にあがります。

自動車のエンジンについている、吸気弁や排気弁はこのようなカムで、開けたり閉めたりしています。

ミシンについているてんびんは、針の動きにつれて上下運動をし上糸をくりだしたり、たぐりあげたりするはたらきをします。

てんびんに、このような動きをさせているのは、てんびんカムです。

てんびんカムは、円筒の外側に、曲がった溝をつけたものです。
てんびんの曲がった部分には、小さなでっぱりがついていてこの溝にはまっています。

このため、てんびんカムが回転するとてんびんは溝の曲がり方にしたがって、上下に動くのです。

このように、カムは、回転運動を往復運動にかえるはたらきをします。
この方法によると、クランク仕掛けよりかんたんになるしカムの形をかえて、往復運動のしかたを、いろいろにかえることができます。

たとえば、止まっている時間を長くしたり、動く速さをかえたり特別な運動をさせたりすることができるので、複雑な機械にはなくてはならないものの1つです。

チェーンと歯車

回転の軸がはなれているところに歯車を使うときは歯車の直径の大きなものを用いるか小さなものならいく組みかく組み合わせて用いなければなりません。

また、ベルトとベルト車のしくみを使えばベルト車がはなれていても、ベルトさえ長くすればよいわけです。

しかし、ベルトとベルト車とでは、滑る場合があります。

ベルトとベルト車の場合の、滑りをなくすためにベルト車に歯をつけベルトのかわりに、歯にかみあうチェーン（くさり）を用いたのがチェーンと歯車（ギヤ）のしくみです。

ふつうのチェーンは上の図のような形になっているのでそれに使う歯車の歯も、ふつうの歯車のものとは、形が違っています。

ふつう、2つの歯車の回転の速さをかえるのに大きさの違う歯車を使います。

そこで、大きいほうを大ギヤ、小さいほうを小ギヤと言っています。

大ギヤと小ギヤの回転の速さ（回転数）は歯車の場合と同じで歯の数で決まります。

小ギヤの歯数が、大ギヤの歯数の2分の1、3分の1、4分の1……なら小ギヤの回転数は、大ギヤの2倍・3倍・4倍……というように反比例します。

回転力も、歯車の場合と全く同じで歯数が多くなれば、それに比例して大きくなります。

チェーンの利用

自転車の後輪をまわすしくみは、チェーンと歯車が使われています。

後輪の軸には、小ギヤがついていてペダルのついているクランク軸に、大ギヤがあります。

大ギヤの歯数と、小ギヤの歯数をくらべると、表のようになっています。

この表で、回転比というのは、両足でペダルを1回ずつ踏み大ギヤを1回転させたときの小ギヤの回転数になります。

荷物をのせるものでは回転比を小さくして力のかけ方が小さくてすむようにしてあります。

また、旅行用自転車のように速く走らせるものには回転比が大きくしてあります。

ふつうの大形自転車では、タイヤの直径が66センチあるので大ギヤを1回転させると後輪は、66ｃｍｘ3.14×2.2 = 約456cm　4.56メートルも進みます。

チェーンブロックには輪をつないだようなチェーンを使い歯車も、それにありような形につくってあります。

時計の歯車

時計は、大きくわけて、針を動かす動力源、その動力を伝える歯車、1秒1秒、時を刻む装置の3つからできています。

大きな柱時計でも、また小さい腕時計でもみなこれらの装置がついていますが内部の装置の大部分は動力を伝える歯車です。

時計では、秒針・分針・時針を決まった回転比で動かすためにいくつもの歯車の組み合わせを使います。

しかし、大きな機械と違って強い力がかからないので平歯車が使われています。

柱時計などにはサシカナという歯車にが使われていますがこれも、平歯車と同じようなはたらきをするものです。

自動車の変速機

自動車が走りだすときや、坂をのぼるときは速さに遅くても強い力を出さなければなりません。

自動車が走り出して、ある速さになってからは車輪の回転が速くても、出す力は小さくてすみます。
また、バックするときは、車輪を逆回転させなければなりません。

このように、動力を車輪に伝える速さや力の大きさ、車輪の回転の向きを加えるしくみが変速機です。

変速機のレバーを動かすと歯車のかみあわせがいろいろかわって、必要な回転がえられるようになっています。

変速機の歯車は車輪に回転が滑らかに伝わるようにはすば歯車でできているのがふつうです。

自動車の減速機と差動機

自動車のエンジンの回転力は変速機にうつされてから推進軸によって、後輪の軸に伝えられます。

推進軸と後輪の軸は直角になっているので丈夫な、はすばかさ歯車が使われています。

この場合、エンジンの回転する速さは、後輪の軸についている大きなかさ歯車で遅くなり、反対に回転力が大きくなります。

このため、この装置を減速機と呼んでいます。

はすばかさ歯車を使うと回転がむらなく伝わり、かみあいも静かです。
また、小さい歯車の中心を、さげてかみ合わせてあるのは自動車の振動を考えて、安定させるためです。

このようにして、後車輪は回転することかできますが自動車がカーブを曲がるときには左と右の車輪の回転速度をかえなければなりません。

このために、差動機と言う仕掛けが使われています。
これには車輪の軸のまわりに回転できる箱の中に4個のかさ歯車がついています。

蒸気タービンの歯車

蒸気タービンから、直に回転運動を取り出すと、回転が速すぎるので歯車で回転速度を落とし、回転力を大きくします。

大きなモーターを使うクレーンでも同じです。

このときの回転は、もちろん、滑らかでなければなりません。
しかし、回転力が大きいので、はすば歯車を使ったのでは軸受に大きな偏った力がかかります。

そこで、大きなやまば歯車を使って、軸受にかかる力をなくしています。

やまば歯車は、このように大きな力のかかる機械に使われ形も非常に大きく、丈夫にできています。

ハンドドリル

ハンドドリルは、金属などの板に、穴をおける機械です。
近頃は、モーターで回転させる電気ドリルが、さかんに使われていますが、値段が安くて、使い方のかんたんなハンドドリルも、まだ多く使われています。

金属に穴を開けるには、よく切れるドリルの刃を金属にあててなるべく速くまわし、金属を削りとります。

このために、ドリルの刃を取り付ける軸に、小さいかさ歯車をつけこれに、大きなかさ歯車がかみあうようにしてあります。

ハンドルで大きなかさ歯車をまわすと小さいかさ歯車によってドリルの刃に、速い回転をあたえることができます。

模型モーターの車の歯車

模型モーターで車をまわすときは、モーターの軸にウォームをつけこれにかみあうウォーム歯車の軸に、車輪をつけます。

これは、モーターの速い回転を落として車をまわす力を大きくするためです。

ウォ－ムを使わないときはかさ歯車、または平歯車の組み合わせを2組以上使わなければなりません。

しかし、ウォームを使うと1組みですみ場所もとらず、しくみもかんたんにすみます。

日よけおろしの歯車

商店などで使っている、日よけをおろしたりまきあげたりするしくみには、綱でまきあげるものかさ歯車を使うものなどがありますが、ふつうに見られるものはウォームとウォーム歯車を使ったものです。

ウォームとウォーム歯車を使ったものでは図のように、ハンドルをまわすと、ウォームがまわります。

するとウォームとかみあうウォーム歯車がまわり歯車の軸といっしょに日よけがまかれたり、おろされたりします。

日よけがあがっているときは日よけの重さでウォーム歯車をまわす力がはたらきます。

しかし、歯車がまわろうとしても、ウォームはまわりませんからどの位置にあってもハンドルをまわさないかぎり、日よけは止まっています。

顕微鏡やカメラの三脚のラックとピニオン

顕微鏡で、レンズの筒を動かす場合には筒のわきについているつまみをまわします。

つまみの軸には、ピニオンがついていて筒にあるラックとかみあっています。
ですから、つまみをまわすと、筒が上下するしくみになっています。

カメラの三脚にもラックとピニオンが使われています。
これも、顕微鏡に使われているラックとピニオンと同じ仕組みになっていて、つまみをまわして、カメラを上下させます。

平歯車

ふつう、どこでも見られる歯車は平歯車といって図のように、2つの軸と歯の向きがみな平行になってします。

①はななめに見た図で、②は、軸に平行な向きから見た図です。

平歯車は、2つの摩擦車が滑らないで回転を伝えるのと、同じはたらきをします。

また、たすきがけのベルトがベルト車とのあいだで滑らないときの回転の伝え方とも同じです。

はすば歯車

はすば歯車には、ふつうの平歯車と違って歯のならんでいる向きが軸の向きと平行になっていません。

そのため、回転を伝えているとき、この傾きからくる力が軸にかかってきます。
そこで、軸のはしに、スラストベアリングという、特別の軸受を使ってこの力をふせいでいます。

やまば歯車

はすば歯車の、軸にかかる力をふせぐために工夫されたのが、やまば歯車です。

これは、ななめになっている面の向きがちょうど反対になっている2枚のはすば歯車を真ん中でだきあわせた形をしています。

こうすると、軸にかかる力は、反対の方向から同じ大きさではたらくので、互いに打ち消されて、力がはたらかないのと同じ結果になります。

かさ歯車

機械のつくりや、取り付ける位置の関係などで回転軸の方向をいろいろとかえなければならないことがあります。

このようなとき、歯の部分が、かさを広げたような形をしたかさ歯車を使うことがあります。

図のようなかさ歯車は、1枚1枚の歯が平歯車のようにまっすぐになっているので、すぐばかさ歯車と言います。

このほかに、はすばかさ歯車や、やまばかさ歯車があります。

ねじ歯車

2つの軸が、互いに直角でも交わらないときは歯のねじれた2つの歯車を、かみあわせたような歯車を使います。

これをねじ歯車と言います。

2つの歯車の軸が、平行でもなくまた、交わりもしないときには食い違い軸歯車を使います。

ウォームとウォーム歯車

回転の向きを直角にだけかえるものにかさ歯車のほかに、ウォームとウォーム歯車があります。

この1組みの歯車の一方は、ねじの形をしたもので、ウォームと言います。
これにかみあう歯車は、平歯車によく似た歯車でウォーム歯車と言います。

ウォ－ムの溝は、一歯おくりと一歯おくりの2種類があります。
一歯おくりは、ウォ－ムが回転するとウォーム歯車を一歯だけおくるもので、二歯おくりはウォームが1回転するとウォーム歯車を二歯だけおくるものです。

ウォームとウォーム歯車は、かさ歯車よりかさばりません。
また、回転の伝わり方は一方的でウォーム歯車をまわしてウォームをまわすことはできません。

ラックとピニオン

回転運動を直線運動にかえて伝える仕掛けにラックとピニオンがあります。

これは平たい帯のようなものの上に、歯形をきったラックとこれにかみあう、ピニオンという歯車からできています。

歯車のはたらき

動く部分がある機械には、ほとんどと言ってよいほど歯車が使われています。
とくに、時計やゼンマイで動くおもちゃなどは歯車ばかりで出来ていると言ってもよいでしょう。

歯車は、摩擦車や、ベルトとベルト車などと同じように回転数や回転の向き、回転軸の方向や回転力の大きさなどをかえて必要な回転運動を伝えるしくみの1つです。

摩擦車と歯車

摩擦車では、2つの車が強く触れ合っていないと滑って空回りすることがあります。
また、伝える力が大きすぎると、まわす力がでないで滑ってしまいます。

この滑りをなくすためには、両方の車のふちに、互いにかみあうぎざぎざの歯をつければよいわけです。

かんたんなものには、はね車のように車のふちに、平たい板を等しい間隔で取り付けたものがあります。

たとえば、おもちゃの歯車には一方に、はね車の形のようなものを他方には、車のふちに鋼線をならべてつけたものがあります。

このような歯車では回転が滑らかにいかなかったり歯の形がすぐ壊れたりして、よい歯車とは言えません。

そこで、精密な機械に使ったり大きな力を伝える歯車には特別な歯をもった歯車がつくられています。

歯車に使われている材料も、その使い道によって、違いがあります。
強い力でかみあう場合には、鋼鉄や特殊のプラスチックでつくります。

それほど力が強くないときには黄銅や、ふつうのプラスチックなどでつくります。

歯車の回転の向きと回転数

2つの歯車を組み合わせて、回転運動を伝える場合その回転の向きは、いつも互いに反対になります。

はじめの歯車と同じ向きにまわしたいときには歯車をもう1つ使えばよいわけです。

回転軸の方向をかえたいときはかさ歯車や、ねじ歯車のような、歯のつけ方の違った歯車が使われます。

回転数は、摩擦車の場合は、車の半径に反比例しますが歯車では、歯の数に反比例します。

たとえば、図のように、Ａ・Ｂの歯車の歯数がそれぞれ60枚と30枚あるとします。

Ａの歯車に動力がついていて、Ａを1回転させると60÷30 = 2で、Ｂの歯車は2回転します。

したがって、Ａが1分間に100回まわれば、Ｂは200回まわります。
面の数が3分の1、4分の1、5分の1……になると回転数は3倍・4倍・5倍……になります。

反対に、歯の数が2倍・3倍・4倍……となれば回転数は2分の1、3分の1、4分の1……になります。

いろいろの歯数のものを、いくつも組み合わせると回転の速さを、必要な大きさにすることができます。

歯車の術の数が多くて数えにくいときには、摩擦車のように半径、または直径をくらべて回転数を決めても、あまり違いはありません。

これは、歯車の中心から、歯と歯がかみあう点までを半径とする円が歯車の歯の数に比例しているからです。

歯車の回転力

歯車の場合も、摩擦車や、ベルトとベルト車の場合と同じように車の半径が大きいほど、回転力は大きくなります。

正確には、回転力は、歯の数に比例します。

たとえば、歯の数が、2倍・3倍・4倍……になれば回転力も2倍・3倍・4倍……となります。

モーターで動くおもちゃの乗り物を調べてみると図のように大小の歯車を使って回転数を小さくし回転力を増やすようにしてあります。

モーターの回転は速いのですが回転力が小さいので、このようにして力をつけているのです。

ぜんまいで動くおもちゃでは、②図のように2組みの歯車で回転数を増し、回転力を小さくしています。

ぜんまいは、強い力で軸をまわしますがこれに歯車を組み合わせると回転力が小さくなり、回転数が増します。

これらの組み合わせ方は、実際の機械にもたくさん利用されています。

摩擦車の利用

摩擦車は、回転力が小さくてもよいところに、多く使われています。

ミシンのはずみ車の、軸受に近いところと下糸まきの車とは、摩擦車になっています。

下糸まきの車のまわりには、ゴムがはめてあり摩擦力が大きくなるようになっています。

普段は、はずみ車の軸とはなれていますが、下糸をまくときにはばねの力で、はずみ車の軸と触れ合うようにしてあります。

電蓄やレコードプレヤーは、ほとんどモーターでレコードをまわしています。

レコードは、その種類によって、1分間に16と2/3、33と1/3、45、78回というように、4種類のものがあります。

そのため、使うレコードの種類によって、回転数を加える必要があり図のような摩擦車のしくみを利用しています。

Ａの車は、モーターの軸につながれています。

これに触れているＢの車は、まわりにゴムをはめこんだ摩擦車でレコードをのせる、ターンテーブルにも触れていてそれをまわす役目をします。

Ａの車は、直径が違う車を、4つ組み合わせたようになっています。
これを上下させて、摩擦車Ｂに触れさせるとレコードの回転数をかえることができます。

エ場で見られるベルト仕掛け

小さな工場へ行くと、そのかたすみにモーターが1台すえてあるのを見受けます。

モーターの軸には、ベルト車がついてして、天井にある大きなベルト車を、幅の広い、丈夫なベルトでまわしています。

大きなベルト車の軸は天井のずっとはしのほうまで伸びていてところどころにある軸受で、支えられています。

この長い軸には、たくさんのベルト車が取り付けてあって軸と同じ速さで回転しています。

そして、その1つ1つのベルト車と下にある機械のベルト車とが、ベルトでつながれています。

このようにして、1台のモーターで工場の中のたくさんの機械を動かします。

そのうちの1台が仕事を休むときは、機械にもう1つ空回りするベルト車をつけておき、それにベルトをうつします。

機械には、回転数をかえてはたらかせたい場合があります。
そこで、大きさの違うベルト車を同じ軸に取り付けて回転数がかえられるようにしてあります。

これを、だん車と言います。

このような工場では、モーターや、大きな摩擦車に故障があると工場中の機械が止まってしまいます。

近頃では、工場で使う機械にもそれぞれ1つずつモーターを取り付けたものが多くなりました。

こうすれば、モーターが故障してもほかの機紙まで止まってしまうことがありません。

そのうえ、天井で、大きな長い軸をまわさなくてすみますしベルトにまきこまれて、怪我をするようなこともありません。

普段見られるベルト仕掛け

小形の機械や、家庭で見られるようなベルト仕掛けでは強い回転力を伝える必要がないので、細いＶベルトやひものようなべルトが使われています。

モーターや発電機の回転は、非常に速いので、ふつうは回転数を落とし回転力を大きくするような、ベルトとベルト車が使われています。

しかし、手や足で動かす機械では、それほど大きな回転力を必要としません。

ただ、手や足であたえた遅い回転をなるべく速い回転にしなければならないので回転数を増すように工夫されています。

ベルトのはたらき

何メートルもはなれているところに回転運動を伝えるには、どうしたらよいでしょうか。

大きな摩擦車を使ってもよいしいくつもの摩擦車を組み合わせてもよいわけですが実際には、なかなかたいへんです。

しかし、下の図のように、動力の回転軸についている車Ａと回転を伝える軸についている車Ｂとのあいだに輪にしたベルトをかければ、かんたんです。

このＡとＢの車のことを、ベルト車（プーリ）と呼んでいます。

ベルトがたるんでいるとＡのベルト車がまわっていても空回りをして、ベルトは動きません。

ベルトが、適当に引っ張られているとベルトがベルト車を押しつけて摩擦力がはたらくようになります。
そのため、ベルト車Ａが回転すれば、ベルトも同じ方向にまわります。

Ｂのベルト車もまた、ベルトとの摩擦でベルトの動く方向にまわりだし、回転運動が伝えられます。

ベルトのかけ方と回転方向

ベルト車にベルトをかけるには、上の図のようなけさがけとたすきがけの、2つの方法があります。

けさがけでは2つのベルト車が同じ向きにまわりたすきがけでは反対向きにまわります。
ですから、場合によって、都合のよいかけ方をすればよいのです。

ベルト車の回転の速さ

たすきがけの場合のベルトを、だんだん短くしていくとしまいに、下の図のような、一組みの摩擦車と同じ形になります。

ベルトを長くして、ベルト車をはなしても、回転のしかたは全く同じです。

このことから、ベルト車の回転の速さはベルトとベルト車のあいだに滑りがなければ摩擦車の場合と全く同じであることがわかります。

一組みのベルト車で、一方のベルト車の半径（または直径）が2倍・3倍・4倍……となれば、回転数は、2分の1、3分の1、4分の1……と減っていきます。

また反対に、半径（または直径）が、2分の1、3分の1、4分の1……と小さくなれば、回転数は2倍・3倍・4倍……と大きくなります。

回転力も、摩擦車の場合と全く同じで、半径の大きなものほど力は大きくなり、半径の小さいものほど力は小さくなります。

ベルトの形

ベルト車をまわすベルトには、その目的によって材質や太さ、切り口の形など、いろいろの種類のものがあります。

これらはいずれも、ベルトにかかる力に応じて力を出しベルト車が空回りしないように選んで使われます。

工場などで、ふつうに使われているものは切り口が平たい帯のようなものです。

ミシンや小形の機械には、切り口がまるいものや四角いもので、ひものようなものが使われます。
これに使うベルト車には、ベルトの断面と同じような溝がついています。

モーターの軸から、直接にポンプなどをまわすとき1分間の回転数が、1000回転以上になることがあります。

このように速い回転のときには、滑りやすくなるので、Ｖベルトと言って、切り口がＶ字形のものを使い、ベルト車にもＶ字形の溝をつけたものを使います。

Ｖベルトは、ベルトとベルト車との触れ合う面積が大きく摩擦力が大きくなります。

そのため、強い力で回転を伝えることができます。

摩擦車のしくみ

電車や自動中が走れるのはレールや道路と車輪とのあいだで摩擦があるからですが、これは摩擦のあるレールや道路の上を車輪が回転するからであるとも言えます。

車体をおさえて、進めないようにしておきレールだけがうしろに動くようなしかけを考えてみるとレールの動きにつれて、車輪だけが回転をはじめます。

図のように、レールを円形に取り付けた台をレコードプレヤーのターンテーブル（回転盤）のようにぐるぐる回転させる場合も同じです。

レールのかわりに、ただの円仮になってもまた、円板のふちに、車が触れていても同じです。

摩擦車は、このように、互いに触れ合っている2つの車の摩擦を利用して、一方の車の回転をほかの車に伝えるしくみのものです。

摩擦車の回転方向

摩擦車は、その車の触れ合う様子によって回転の向きが、いろいろとかわることがあります。

つぎの図の①の場合は、2つの車の軸が平行でそれぞれ車の外側で触れ合っています。

このときは、Ａの車が矢印の方向にまわっているとＢの車は反対の向きにまわります。

②の図のように、大きな車Ｂの内側に、小さな車Ａが触れ合っているときはＡの車が矢印の方向に回転すると、Ｂの車も同じ方向に回転します。

③の図の場合は、Ａの車の軸と、Ｂ・Ｃ・Ｄの車の軸が互いに心角になっています。

大きな車Ａが矢印の方向に回転しているとき、Ｂ・Ｃ・Ｄの車は①図や②図のように、いちがいに、同じ向きとか反対向きにまわるとは言えません。

この場合は、それぞれの車が、Ａの車の触れ合っている点のところで①図のような関係で回転していると考えるとよいでしょう。

摩擦車の回転の速さ

ある時間、たとえば1分間に車が何回まわるかという数を回転数と言います。
回転数が大きいということは、車が速くまわるということです。
したがって、回転数の大小で、回転の速さをくらべることができます。

2つの中が同じ大きさのときは、その半径は同じです。
車が滑らないでまわるならば、一方の車が1回まわるともう一方の車も、1回まわります。

これは、反対向きにまわしても同じです。

下の図で、Ｂの車の半径がＡの車の半径の2倍だとするとＢの車の円周はＡの車の円周の2倍になります。

したがって、Ｂが1回まわると、Ａは2回まわります。
同転数でいうとＡはＢの2倍です。

Ｂの車の半径が、Ａの3倍・4倍……に増えると、Ａの車の回転数は、Ｂの3倍・4倍……となります。これは、回転の向きに関係しません。

このことから、車の回転数（回転の速さ）は半径の大きさに反比例するということがわかります。

まえの図の③の場合でもＡの車の中心から触れ合う点までの距離を半径とすれば、同じことが言えます。

摩擦車の回転力

摩擦車の回転数は、触れ合う2つの車のうち半径が小さいほうが大きくなり半径が2分の1、3分の1、4分の1……になると回転数は2倍・3倍・4倍……となります。

ところが、伝えられる回転の力は、これと全く反対になり回転数の大きいほど、回転の力は小さくなります。
車の大きさで言えば、車の半径が小さいほど回転を伝える力は小さくなり、半径の大きさに比例します。

ミシンの下糸をまくときなどのように回転の力は小さくても速く回転させたいときには、小さい摩擦車を使います。

大きな回転の力を伝えたいときは、伝える車の半径を大きくしなければなりません。

しかし、力を大きくしようとすると、滑って空回りすることがあります。
このようなときは、別に歯車のような便利なものがあるので摩擦車はあまり使われません。

摩擦の減らし方

摩擦は、いろいろと役に立ちますが、重い物を動かすときなどは摩擦があるために、たいへん骨が折れます。

このようなときは、できるだけ摩擦を小さくする工夫をしなければなりません。

ころと車

摩擦のうち、物が動きだすときにはたらく最大摩擦力がいちばん大きく、つぎに滑り摩擦、いちばん小さいのが転がり摩擦です。

マッチ箱を動かす実験で、マッチ箱の下に、まるい鉛筆を入れると小さな力でも、マッチ箱が動きだしました。

このように触れ合う面のあいだに、まるい棒を入れて引っ張ると転がり摩擦になるので何10分の1という小さな力で物体を動かすことができます。

このまるい棒のことをころと言います。

城の石垣を見ると、すばらしく大きな石があります。
これは、ころを使って運んだものですが、いまでも、家か動かしたり重い機械などを近くに運ぶのに、ころが使われています。

ころか使って物を運ぶには、つぎつぎところをまえにならべていかなければなりません。
この不便をなくすために、1本の軸の両はしに、輸をはめたものが車です。

また、ころの軸をかわくにとりつけて帯のようにならべたものがあります。
これは、ローラコンベアと呼ばれるもので流れ作業の進んでいる工場などで、よく使われています。

ころも車も、転がり摩擦力のほうが滑り摩擦力よりはるかに小さいことを利用したものです。

そこで、転がり摩擦について、つぎのような実験でもう少しくわしく調べてみましょう。

実験

ちょうど同じ形につくった、2本の四角い木の棒をレールのように平行にならべて、その上に、直角にころをおきます。
そして、この四角い棒と、ころのあいだの転がり摩擦を調べてみましょう。

木の棒のかわりに、2つの机を、少しはなして平行にならべその上にころを載せると回じ仕掛けがかんたんにつくれます。

まず、同じ重さの2つの重りにひもをつけてころに2,3回まきつけてつるします。

このとき、ころは、重り2つだけの重さところの重さを加えた力で木の棒を押していることになります。

つぎに、一方の重りにさげた皿に、少しずつ砂を載せていきます。
すると、ころと木の棒とのあいだに、転がり摩擦があるためしばらくは転がりませんが、砂がある重さになると、転がりはじめます。

この実験で、ころが転がりはじめたときの、砂の重さを測ります。
そして、2つの重りと、ころの重行を加えたもので、砂の重さを割るとこのときの摩擦係数がわかります。

ころと同じ材料で、同じ重さの四角い切れ端をつくり滑り摩擦係数を測ってみると転がり摩擦係数の100倍も大きいことがわかります。

軸受と油

車には転がり摩擦のほかに車軸と軸受のあいだにはたらく摩擦もあります。
車軸は軸受の中で滑りながら回転しますから、この摩擦は、滑り摩擦です。

雨戸や障子が開けにくいときろうや油をぬると、軽く開けられるようになります。
また、机や、たんすの引出が開けにくいときにも、ろうをぬります。

これは、面のでこぼこのうちへこんだところを、ろうや油がうずめて、面を滑らかにするからです。

軸と軸受のあいだには、油をさして、摩擦を小さくします。

軸を軸受に入れると、軸の両側に、角笛の形をした、隙間ができます。
ここに油を入れて、軸を回転させると油は、軸の表面にひきずられて隙間の広いところから、せまいところに向かって、流れこみます。

これは、油にねばりけ（ない）があるからです。

このとき、油に軸と軸受の触れ合う面を引き離そうとする力がはたらきます。
そのため、軸は油の上に浮いているようになり、軸と軸受の摩擦がふせげます。

油と金属とのあいだにも、摩擦はあります。
しかし、金属どうしの摩擦にくらべれば、ごく小さいものです。

図は、貨車に使われている、軸受です。
この場合は、貨車の重みに、車軸の上からかかっています。

そこで、車軸の上側に、やわらかい貴族（ホワイトメタル）をもった軸受がねをつけています。

車軸の下には、油をしみこませた、糸くずがつめてあります。
油は、車軸が回転するにつれて、自然に車軸と軸受のあいだに入っていきます。

ボールベアリングや、ローラベアリングのように、強い圧力がかかって速く回転するものには、ねばりけの大きい、のりのようなグリースをつめ、摩擦熱によって、焼きつかないようにしています。

ボールベアリング

軸受の摩擦は、油々さすことによって、小さくすることもできますが滑り摩擦を、転がり摩擦にかえて、摩擦を小さくすることもできます。

外から見たのではわかりませんが、自転車や自動車の軸受には小さい鋼鉄の球をたくさん入れたものを使っています。

これは、ボールベアリングといって、車軸と軸受が、直接触れ合って滑り摩擦を起こすかわりに、ボールが転がって転がり摩擦になるようにしたものです。

滑り摩擦でも、転がり摩擦でも触れ合う面が滑らかでないと摩擦が大きくはたらきます。
この摩擦を小さくするには、面をできるだけ滑らかにすることが大切です。

砂利をしいた道路よりも、アスファルトやコンクリートで舗装した道路のほうが自転車や自動車が走りやすいのは、このためです。

また、汽車や電車が走るレールも、転がり摩擦を小さくするために工夫されたものです。

軸や軸受も、できるだけ滑らかに磨かなければなりません。
ボールベアリングの表面も、非常に滑らかにしてあります。

自転車や自動車では、車のまわる速さはそれほど大きくありません。
しかし、飛行機のプロペラのように、すごい速さで回転するものはボールの表面が、摩擦熱で溶けることがあります。

このようなときは、摩擦がぐっと大きくなります。
それで、高速回転をするボールベアリングについてはその材質をとくに工夫してあります。

ローラベアリング

大きな力のかかる軸受では、球のかわりに小さいころをならべた、ローラベアリングを使います。

ころは、円錐形・球面・円筒形などのものが使われています。
左の図は鉄道車両に使われている、ローラベアリングの一種です。

摩擦の利用

摩擦は、邪魔になることもあれば、役に立つこともあります。
私たちが地面を歩けるのは、地面と足とのあいだに、摩擦があるからです。

本やえんぴつを、手で握っていられるのも、摩擦があるからです。

また、ひもを結んだとき、ひとりでにとけないのも釘で板を止めることができるのも、摩擦がはたらいているからです。

このほか、摩擦を上手に利用して私たちの生活に役立てているものが、たくさんあります。

ブレーキ

自転車のブレーキは車輪のリムを硬いゴムで押しつけるようになっています。
これは、ゴムの摩擦が大きいことを利用しています。

また、もっと大きな力で車輪の回転を止めるためにハンドブレーキが使われています。

これは、摩擦の大きい石綿を材料にしてつくった帯（ブレーキバンド）で、鋼鉄の輪をしめつけるものです。

スクーター・オートバイ・自動車などのように速く走る乗り物を止めるためにはさらに大きな摩擦力を出さなければなりません。

そこで、鋼鉄製のブレーキドラムの内側に固い石綿織物をはったブレーキシューを大きな力で押しつけるしくみを使っています。

また、汽車や電車などでは、制輪子という鉄を車輪に押しつけて止めます。

スノーチェーン

雪が降ると、バスなどの自動車は、タイヤにチェーンをまきつけます。

これは、雪によって、タイヤがスリップしやすくなるためにタイヤにチェーンをまきつけ、道路とのあいだの摩擦を大きくして滑らないようにするためです。

チェーンのついていない自動車は、スリップしてたいへん危険です。

このように、摩擦は、私たちの生活に上手に利用されています。

滑り摩擦

スキーでもスケートでも、滑りはじめには最大摩擦力に打ち勝たなければならないので、大きな力を必要とします。

しかし、滑っているあいだは、運動摩擦力がはたらいているのであまり力を加えなくても滑り続けます。

このように、ある面を滑るときの摩擦を運動摩擦のうちでも、とくに滑り摩擦と言います。

転がり摩擦

まえの摩擦用の箱の実験で摩擦用の箱のかわりに斜面用のトロッコをつないでみます。
すると、さらの重さだけでトロッコは動きはじめます。

この場合、トロッコが板の面を転がって動きます。
このときの摩擦を、転がり摩擦と言います。

転がり摩擦力は滑り摩擦力より、さらに小さいので摩擦を減らす方法として機械の部分などに広く利用されています。

摩擦係数

摩擦用の箱で、板と接する面をいろいろかえてみると最大摩擦力は、まえと違った大きさになります。
つまり、箱の4つの面のうち2面は同じ性質で、接している面積が違います。

箱の広い面を接するときと、せまい面を接するときの実験をしてみるとせまい面のときの最大摩擦力と広い面のときの最大摩擦力は同じ大きさになります。

これらの実験から、最大摩擦力は、触れ合う表面の性質によって大きさが違いますが、面の広さには関係がないことがわかります。

つぎに、箱の上に分銅をのせて、重さをまえの2倍にし同じように最大摩擦力を測ってみると、2倍になっているのがわかります。

皿に分銅を増やして、摩擦用の箱を重くすると最大摩擦力も、それに比例して増えていきます。

このことから、最大摩擦力は、2つの面の押し合う力に比例していることがわかります。

紙の面と、紙やすりの面とでは、最大摩擦力が違います。
それは、表面の性質が違うからです。
この表面の性質は、摩擦係数という数であらわします。

図のような実験をしてみましょう。

箱が動きだす瞬間は、箱を引く力Ｐと最大摩擦力Ｑとは等しくなります。
触れ合っている2つの面の押し合う力を、ＲとＳとしますとＱの力とＳの力の比を、摩擦係数と言います。

同じ重さの物なら、摩擦係数の大きい物ほど動かすのに余計に力がいります。
また、動いているときでも、重い物ほど、大きな摩擦力がはたらきます。

上の表は、いろいろな物の、摩擦係数をあらわしたものです。
触れ合う面の違いによって、摩擦係数の大きさもだいぶ違うことがわかります。

摩擦の起こるわけ

2つの面のあいだに、どうして摩擦が起こるのでしょうか。
これについては、つぎのような原因が考えられています。

①　2つの面の直接ふれあう部分がくっついてしまい、それを引き離すのに、力がいる。

②　物の表面は、どんなに滑らかに見えても非常に細かいでこぼこがあり、これが互いに噛みあうので、それを乗り越えたり引きちぎったりするために、力がいる。

③　硬い面が、柔らかい面の上にあるときは硬い面が、柔らかい面を掘り起こしたり、壊したりするために力がいる。

この様子は、触れ合う物によって、それぞれ違うので摩擦力の大きさも、いろいろかわるのです。

摩擦力

机の上にある本やスタンドを、軽く押してごらんなさい。
わずかの力で押したのでは動きませんが、強く押すと動き出します。

物を動かすには、力を加えなければなりません。
しかし、加える力が、ある大きさより小さいとこのように物が動かないことがあります。

力を加えているのに物が動かないほかの例を考えてみましょう。

ふたりが向き合って、1本の棒を両はしから互いに押したとします。
ふたりの押す力の大きさが等しくて向きが反対なので棒はどちらへも動きません。

机の上の物も、これと同じです。
物を押しても動かないのは、動かす方向と反対に別の力がはたらいていて、動くのを止めているからです。

このときの力は、目には見えませんが触れ合っている2つの物の面のあいだにはたらいている力で摩擦、または、摩擦力と言います。

このように、摩擦力は、物の運動をさまたげる方向にはたらくので摩擦力より大きな力で押したり引いたりしなければ物を動かすことはできません。

雪や氷の上では、よく滑ります。これからです。

しかし、スキーで滑る場合でも、板の上ならともかく平地で滑るときには、ときどき手や足に力を加えて加減しないと続けて滑ることができません。

力を加えないでいると、まもなく止まってしまいます。

このことから、滑っているときでも運動をさまたげろ力は小さいけれども、
はたらいてしることがわかります。

走っている自動車や電車は、動きだしてからもたえずエンジンやモーターをはたらかせています。
これは摩擦力によって、自動車や電車の運動が絶えずさまたげられているためです。

このように、摩擦力は物が止まっているときばかりでなく滑っている物や転がっている物にもはたらいてその動きを止めようとしています。

実験

摩擦力の大きさを調べるには、図のような摩擦実験装置を使います。

摩擦用の箱は、4つの面がそれぞれすべすべする金属の面と金属に紙をはった面、紙やすりをはった面、もう1つの面は板に接している面積が少なくなっています。

摩擦用の箱と皿を、滑車を通して写真のようにつなげます。
つぎに、箱が滑り出すまで、さらに分銅を載せていきます。

このとき、摩擦用の箱には、分銅と皿の重さのために上の図のようにＰという水平な力がはたらきますが、まだ動きません。

これは、Ｑのような水平で、Ｐと反対向きの摩擦力がはたらきＰとつりあっているからです。

さらの分銅を増やせば増やすほど、箱を引く力Ｐは大きくなります。
しかし、摩擦力もだんだん大きくなります。
この2つの力の大きさが同じで、いつもつりあっているときは箱は動きません。

摩擦力の大きさは、面の材質によってもまた、斜面の角度によっても、かわってきます。

静止摩擦力

物体が止まっているときの摩擦はその物体を引く力と大きさが等しく向きが反対です。

たとえば、1キログラムの力で引いても動かないときは1キログラムの摩擦力がはたらいているわけです。

まえと同じ実験で、ある重さまで分銅を載せると、ついに箱が動きはじめます。

摩擦力は、これ以上大きくなりません。
つまり、摩擦力は、箱が動きはじめようとするときが、いちばん大きいのです。

物体が止まっているときに、はたらく摩擦力を静止摩擦力と言い物体が動きだす瞬間のいちばん大きな摩擦力を最大（静止）摩擦力と言います。

最大摩擦力の大きさは、このときの皿と分銅の重さと等しくなります。
したがって、それを測りで測れば、最大摩擦力がわかります。

運動摩擦力

静止摩擦力に対し、物体が動いているときにその動いている物体を止めようとする摩擦力を運動摩擦力と言います。

運動摩擦力は、最大摩擦力より小さくなっています。

この運動摩擦力の大きさは物体の速度の大きさにはほとんど関係かわりません。

ねじと斜面

ねじも、斜面のはたらきを利用したものです。
ねじを見ただけでは、斜面とどんな関係にあるかよくわかりにくいので、つぎのような実験をしてみましょう。

紙を、細長い直角三角形に切って写真のように鉛筆にくるくるとまきつけます。

すると、直角三角形の長い辺（斜辺）は、ねじの形になります。
右側のものは針金を直角三角形をまくのと同じようにまきつけたものです。
こうすると、いっそうねじらしい感じがします。

このことから、ねじは、円柱のまわりに斜面をまきつけてつくったもので、ねじの山のところが、斜面にあたることがわかります。

この斜面は、ねじの一方のはしから、他のはしまで続いているのでひとまきだけ取り出して考えることにします。

ひとまきだけを取り出しても、やはり直角三角形でその高さは、下の図のＢＣにあたります。

このＢＣの長さは斜面をもういちどまきつけて進む高さ、ＣＤと同じです。

ですから、このねじは、1回まわるたびに小さい三角形の高さ、ＢＣぶんだけ上へ進みます。
この長さをピッチ、または、ねじの歩みと言います。

ねじの高いところを山、低いところを谷と言います。
山と山、谷と谷のあいだの長さが、ピッチになります。

ねじのはたらき

ねじは、円柱のまわりにつくった斜面ですからそのはたらきは、斜面のはたらきと同じに考えられます。

下の図で、Ａにある物は、ねじをひとまわりさせるとＡＣの斜面にそって、Ｃまで上がります。
これは、ねじの1ピッチぶんだけ引き上げられたことになります。

さらにひとまわりさせると、Ｃにある物は、Ｅまで引き上げられます。
ＤＥの高さは、ＢＣの2倍で、ねじの2ピッチぶんにあたります。

ねじのはたらきは、このように斜面を使って物を持ち上げるのと同じです。
したがって、ピッチが小さいほど、ねじの斜面はゆるやかになりいっそう小さな力で大きな力を出すことができます。

ねじの出す力

直径が10ミリで、ピッチが2ミリのねじの出す力を考えてみましょう。

このとき、ひとまきの長さは、31.4ミリ（直径の3.14倍）になり斜面の長さは、約31.5ミリになります。

まえの図で、ＢＣの長さが2ミリ、ＡＣの長さが31.5ミリの直角三角形について斜面の力を考えればよいのです。

このねじに加える力は、斜面の上の物をＡからＣまで斜面にそって引き上げる力にあたりねじの出す力は、物をＢからＣまで上げる力です。

ですから、ねじに加える力と、ねじの出す力との割合は斜面の高さ（ピッチ）と、斜面の長さ（ねじのひとまわりぶんの長さ）との比であらわされます。

たとえば、このねじに1キログラムの力を加えたとすると、

1kg :（ねじの出す力）＝ 2 : 31.5

（ねじの出す力）＝ 1kg × 31.5/2 ≒ 約15.8kg

ねじの出す力は、約15.8キログラムになります。
しかし、ねじをまわすには、万力のように、多くはとってがつけてあります。
ねじの半径の10倍の長さのとってがつけてあると、直接ねじをまわすより、10分の1の力で同じ力を出させることができます。

ねじのいろいろ

ねじには、ねじの切り方や、ねじ山の形によってつぎのような種類があります。

おねじ・めねじ

円柱の外側に、直角三角形の紙をまきつけた形のものがおねじ、円筒の内側に、直角三角形の紙をまきつけた形のものが、めねじです。
言い換えると、棒になっていて、ねじこむほうがおねじ、ねじ穴が開いているほうが、めねじです。

右ねじ・左ねじ

ねじのまわる方向と進む方向から、右ねじと左ねじにおけることができます。

時計の針のまわる方向（右まわり）にまわすとまえに進むねじは、右ねじです。

これと反対に、左にまわすとまえに進むねじは、左ねじです。
ふつうのねじはたいてい右ねじで左ねじは特別の場合にしか使われていません。

三角ねじ

ボルト・もくねじなどのねじ山は、三角形をしています。
このようなねじを、三角ねじと言います。

三角ねじは小さな力でも物をしっかりと締め付けられるので、広く使われています。
もくねじのねじ山は、刃物の役目をして、仮などにくいこんでいきます。

マイクロメーターやコンパス・からすぐちなどの調節ねじも三角ねじです。
この場合は、物を少しずつ正確に動かす役目をします。

角ねじ

万力・ジャッキなどのねじは、ねじ山が四角になっています。
このようなねじを、四角ねじ、または角ねじと呼んでいます。

角ねじは、ねじに大きな力を出させるところに使います。
三角ねじを使ったのでは、ねじ山が潰れて、役に立たなくなるからです。

くさびのはたらき

斜面を使うと、小さい力でも、重い物を引き上げることができます。
つまり、小さい力で大きな力を出したことになります。

くさびは、この斜面の性質を利用したものです。

くさびのきり口は、たいてい2つの辺の等しい、細い三角形をしています。
この二辺にはさまれた角をくさびの角、短い一辺をくさびの頭と言います。

下の図をごらんなさい。

ハンマーなどで、くさびの頭にＰの力を加えるとこの力は、くさびの斜辺に直角な2つの力、ＱとＲとにわかれます。

この力が、木を折るときの力になります。

この3つの力のあいだにも、斜面のときと同じように力の平行四辺形があてはまります。
平行四辺形の対角線Ｓは、Ｐと同じです。

この平行四辺形の半分の三角形は、くさびと同じ角度をもっているのでＲとＳの大きさの割合は、くさびの斜面と頭の長さの割合に等しくなります。

（Ｒの力）：（Ｓの力）＝（斜面の長さ）：（頭の長さ）

Ｒの力は、くさびの出す力ですから、これを式であらわすと、

Ｒ……くさびの出す力
Ｓ……加えた力

この式からわかるように、くさびの頭の長さが、斜面にくらべて短いほど、くさびは大きな力を出すことができます。

たとえば、くさびの斜面の長さが、頭の長さの5倍あったとします。
このくさびに1キログラムの力をはたらかせると5キログラムずつの力となって、2つの斜面からはたらきます。

くさびと刃物

斧や、包丁などは、その切り口を見るとちょうどくさびと同じ形をしています。

物を割ったり、切ったりするときの力のはたらき方も、くさびと同じです。

刃物は刃がうすいほど、切れ味がよくなります。
それは、くさびの角度が小さいほど、くさびの出す力は大きくなるからです。

しかし、刃がうすいと折れやすくなるので使い道によって、いろいろとかわった形にしています。

くわ・すき・つるはし・スコップなど地面を掘り起こす道具もくさびと同じに考えられます。

これらの道具の形と厚さ、えと刃の角度、地面の硬さなどとの関係を調べてみるのも、おもしろいでしょう。

かんな・のみなど、材料に食い込んで削っていくときの力のはたらき方も、くさびと同じです。

包丁やナイフは、ただ上から押しつけて切るよりも押したり、引いたりするほうが、よく切れます。

下の図をごらんなさい。

包丁を手もとに引きながら切ると、包丁の動きは、Ｒの方向になります。
このときのくさびの形は、（Ａ）のようになります。
包丁を、ただ上から押したときのくさびの形は（Ｅ）です。

この2つのくさびを調べると、くさびの頭の長さは同じでも手もとに引いたときのほうが、斜面の長さはずっと長いことがわかります。

斜面が長くなると、くさびの角度は小さくなりますからよく切れることになるのです。

斜面の力をもとめる方法

まえの実験からでは、摩擦があるので正しい力の大きさをもとめることはできません。
そこで、斜面にそって落ちる力を正しくもとめる方法を考えてみましょう。

斜面の力をもとめる方法には、図を書いてもとめる方法と計算でもとめる方法の2通りがあります。

図を書いてもとめる方法

この方法は、力の大きさをあらわすのに矢印を使い、矢印の方向は力がはたらいている方向とします。

矢印の長さは、力の大きさの割合をあらわすように書きますたとえば、1キログラムを1センチの長さであらわしたとすると5センチの矢印は、5キログラムをあらわすものとします。

下の図のように、斜面の傾きを30度として斜面の上に3キログラムの物体を載せます。

この場合、物体にはたらく重力のＷは、真下に向かってはたらきます。
このとき、０Ｗの力は、斜面にそって落ちようとする力ＯＰと物体が斜面に垂直におさえつける力ＯＱの2つの力に分解されます。

このＯＱという力の反作用として、抗力ＯＱ’がはたらいています。

重力ＯＷを対角線としＯＰとＯＱの力を二辺とする平行四辺形をつくってみます。
ＯＷの長さとＯＰとＯＱの長さを測ると力の大きさの割合がもとめられます。

たとえば、上の図で斜面の上に3キログラムの物体の重力ＯＷを3センチであらわしたとするとＯＰの力の大きさは、15センチであらわされます。

また、45度の斜面の上の物体は下の図のように30度の斜面の上の物体よりも滑りやすくなります。

これは、30度の斜面の上においた物体と同じ重さの物体を45度の斜面の上に置いてみるとわかります。

つまり、30度のときのＯＰと45度のときのＯＰとでは45度のときのＯＰのほうが大きいのです。

計算でもとめる方法

ＯＰの力は、計算によっても、もとめることができます。

物体の重さの中心をＯとして、まえと同じような図を書いてみましょう。
重力ＯＷの矢印と、斜面にそって落ちようとする力ＯＰの矢印と出てきた三角形ＯＷＰをもとの三角形ＡＢＣとくらべてみましょう。

この2つの三角形では、角Ｂと角Ｗが30度、角Ａと角Ｏが60度、角Ｃと角Ｐが直角でそれぞれ等しくなっています。
この2つの三角形は、3つの辺の長さの割合が同じになります。

つまり、ＯＷの力とＯＰの力の大きさの割合は斜面をつくっている三角形ＡＢＣの、傾いた辺の長さ（ＡＢ）と垂直の辺の長さ（ＡＣ）との割合に等しくなります。

これを比例式であらわすと　〇Ｗ　:　ＯＰ = ＡＢ　:　ＡＣ　となります。

これを変形すると　ＯＰ＝ＯＷ × ＡＣ/ＡＢ　となります。

たとえば、30度の傾きをもった斜面ではＡＢの長さと、ＡＣの長さの割合は、2対1です。
いま、この斜面に3キログラムの物体をのせると　ＯＰ＝ 3(kg) × 1/2 ＝ 1.5(kg) となりまえと同じく、1.5キログラムになります。

傾いた辺の長さと、垂直の辺の長さを測って、その割合をもとめておくと、ＯＷがどのような値でも、ＯＰがもとめられます。

斜面と仕事

斜面を使って、物体を引き上げたときにする仕事もてこや滑車・輪軸を使ったときにする仕事と、原理は同じです。

つまり、力では得をしていますが、距離で損をしています。

たとえば、4キログラムの物体を人の手で1メートル持ち上げたときにした仕事の量は　4(kg）× 1(m）= 4(kgm) となります。

これを30度の斜面で引き上げたときの仕事を考えてみましょう。
斜面の上に4キログラムの物体を落ちないように支えるには、上の公式から　Pの力 ＝ 4(kg) × 1/2 ＝ 2(kg)　で、つまり、2キログラムの力で反対の向きにくわえればちょうどつり合うことになります。

30度の斜面の距離は、高さの2倍の距離がありますから1メートル上げるには、斜面の上を、2メートル動かさなければなりません。

ですから、30度の斜面で、物体を1メートル引き上げたときの仕事の量は、　2（kg)× 2(m）= 4(kgm）となります。

したがって斜面を使わないで、物体を持ち上げるときにする仕事も斜面を使って、それと同じ高さまで物体を引き上げるときにする仕事も仕事の量としては、かわりがありません。

しかし、実際には、斜面を使った場合には斜面と物体とのあいだで、摩擦がはたらいているのでその分だけ余計に力が必要です。

図は、物体の重さが一定なときに、斜面の角度をかえることによって引き上げるときの力の大きさの違いを、矢印であらしわしたものです。

斜面

平らな道を歩くときよりも坂道をのぼるときのほうが余計に疲れます。
急な坂道をのぼるよりも傾斜のゆるやかな坂道のほうが疲れは少なくてすみます。

たとえば、山にのぼるとき、頂上がすぐ目の前に見えてしてもまっすぐに頂上までのぼろうとするには、たいへんな労力が必要です。

そこで、多くの人が遠まわりをしてでも傾斜のゆるやかな道を選んで、のぼるわけです。

そのほうが、歩く道のりは長いけれども疲れは、ずっと少なくてすむからです。

スキーで、雪の上を滑るときは、どうでしょうか。
平らなとこらでは、自然に滑るわけにはいきません。
ところが、斜面にそって滑ると、勢いよく雪を蹴って進みます。

このように坂道は平地と違っていろいろなはたらきをすることがわかります。

坂道は、必ず、ある角度の傾きを持っています。
このように、傾いている面を斜面と言います。

斜面にはたらく力

私たちは大きいカを出すと疲れますが小さい力では、それほど疲れません。
坂逆を歩くときに平地を歩くときよりも、余計に疲れるのはそれだけ大きい力を出しているからです。

平らな机の上に、滑りやすい物または、転がりやすい物をおいても、そのままの位置で止まっています。

ところが斜面の上におくと自然に斜面にそって滑り落ちたり、転がり落ちたりします。

斜面の上では、このように力を加えなくても自然に物を動かす力がはたらいています。

これは、物が真下に落ちようとすると斜面が邪魔をするため、真下に落ちず、斜面に沿って下に落ちるからです。

物体が真下に落ちる速さと、斜面に沿って落ちる速さとをくらべてみると、斜面に沿って落ちるほうが、ずっと遅いことに気がつきます。

斜面の角度をいろいろかえると斜面に沿って落ちる速さがまわります。
それは、斜面の角度によって斜面にそって物体にはたらく力がかわるからです。

実験

写真のような斜面の実験装置を用意します。

①　まず、45度の斜面で実験してみましょう。
重りのいろいろかえて、斜面の上の物とつり合わせると
物体は上にも下にも動かないで止まります。

②　つぎに、斜面の角度をだんだん小さくして
30度にした場合を考えてみましょう。

重りの重さはそのままで、斜面の角度を、かえただけです。
この場合、斜面の上の物体が、斜面の上部にのぼっています。

③　今度は斜面の角度を大きくして、角度を60度にしてみましょう。
斜面の上の物体は、30度の場合とは反対に、斜面の下部へ落ちています。

④　斜面の角度が直角（90度）になったときは
ちょうど物体をつりあげたときと同じになります。

したがって、斜面の上の物体が下に落ちようとする力は
このときがいちばん大きくなります。

また、重りの重さが、斜面の上の物体の重さと等しいとき、つりあいます。
右の図は、45度・30度・60度・直角の斜面の実験を1つにしたものです。

これらの実験で、斜面の角度が、大きくなるほど
斜面にそって落ちようとする力も大きくなることがわかります。

水平面にある物体は、ある方向に力を加えないと動きませんが
斜面の上では、力を加えなくても自然に動きます。

これは地球に物体を引き寄せる力が、はたらいているからです。
そのため、地球上の物体は、必ず地表に落ちます。
物体にはたらく下向きの力で物体の重さとなる力を重力と言います。